核分裂
核分裂の発見
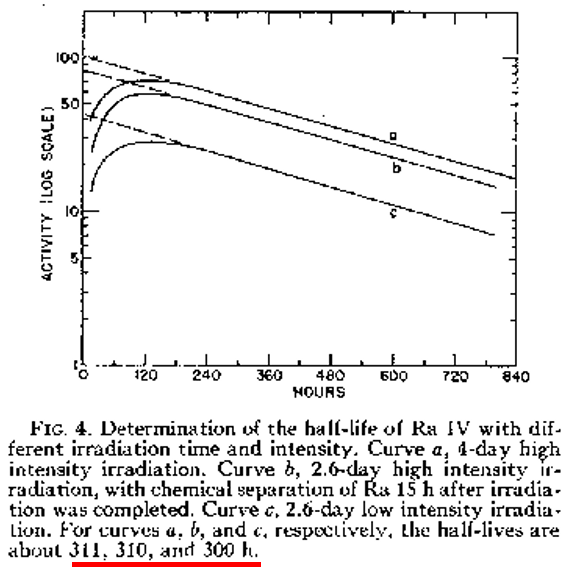
図1 Hahnらの半減期決定実験の結果の図
1938年、ベルリンのHahnらのグループはUを中性子で照射する実験からBa(バリウム)を発見したのだが、この時生成核種がBaだとは考えていなかったため、生成核種の半減期を調べる実験を行った。図1はその実験結果を示している。中性子照射量の異なる複数の実験結果から生成された核種の半減期が300~311時間のいずれかであることが分かった(図の脚注にも示されている)。実際は、この時の反応は235U(235の重さのU、同位体については(リンク先)を参照)に中性子を照射して140Baと93Kr(クリプトン)に分かれる反応であった。140Baの半減期は、現在306時間と分かっており,実験結果で得られた半減期はこれとほぼ一致していた。この反応において最終的に200 MeVくらいのエネルギーを放出するが、このエネルギーは原子核の性質で述べた、Bethe-Weisaeckerの質量公式(リンク先)で計算できる。
核分裂の概要
Uには、低エネルギー中性子で核分裂しやすい235Uとそうでない238Uという同位体素がある。天然Uには235Uは0.7%しか含まれていない。この235Uが中性子を吸い込むことで核分裂が発生し、平均で2.5個の中性子と共に約200 MeVのエネルギーを生じる。核分裂でエネルギーが発生するのは、図2の原子核の結合エネルギー(リンク先)で説明できる。弱く結合した原子核から強く結合した原子核へ移行する際に質量の一部が失われ、その質量に相当するエネルギーが発生する。そのエネルギーは、有名なアインシュタインの質量エネルギー等価式E=mc2(https://ja.wikipedia.org/wiki/E%3Dmc2)で算出できる。図2からUの領域では、核子当たりの結合エネルギーは、およそ7.6 MeV程度、核分裂生成物(Aが120程度)の核子当たりの結合エネルギーは8.5 MeV程度であるので、その差に核子数(原子核を構成する陽子及び中性子の総数)を乗じて、235Uが中性子を吸収して分裂した時のエネルギーを計算することが可能である。生じるエネルギーは、およそ210 MeV程度であり、その内訳(表1)はほとんどが核分裂片の運動エネルギーである。
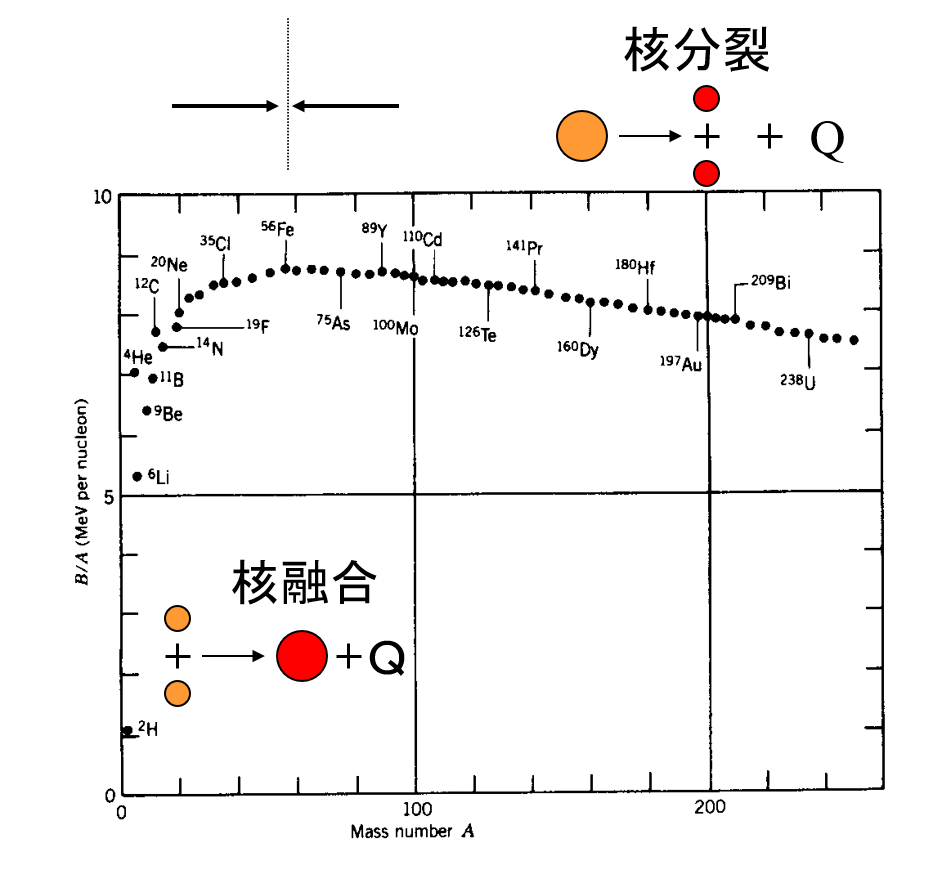
図2 原子核の結合エネルギー
核分裂は、液滴モデル(原子核を「ぶよんぶよん」した水滴に見立ててその性質を記述するモデル、https://ja.wikipedia.org/wiki/%E6%B6%B2%E6%BB%B4%E6%A8%A1%E5%9E%8B)による安定性(バラバラにならない)の限界によって説明できる。原子核が安定に存在する限界について、表面張力(引力)と+の電気を帯びる陽子同士のクーロン(斥力)が釣り合っていることを考える。原子核内の陽子数と中性子数がほぼ等しい軽い核は球形であるが、中性子数が陽子数の1.5倍程度あるウランの領域では原子核は球形から変形している方が安定になる。表面エネルギーとクーロンエネルギーの釣り合いを考えると、 x=約(Z2/A)/50で求めることができるfissilityパラメータという量が導くことができ、xが大きい程核分裂が起こりやすく、核分裂の起こりやすさの指標となる。Uより原子番号(=陽子数)の大きい元素が天然に残っていないことの一つの原因となっている。xが1以下であれば安定で、さまざまな原子核のfissilityパラメータを計算すると表2のようになる。ちなみに、液滴モデルによる安定性の限界はZが120程度となる。実際には、殻効果(リンク先)が安定性に大きく影響する。
核分裂障壁
同じUであるにも関わらず、中性子エネルギーが低い領域では、238Uの中性子核分裂断面積(核分裂反応の起こりやすさを中性子の当たり易さという視点から面積の単位で示した物理量)は、235Uにくらべて小さいことが分かっている。図3に235Uと238Uの中性子核分裂断面積を示す。縦軸の断面積σの単位をb(バーン)で表しているが、1b=10-24cm2である。235Uは中性子核分裂断面積が大きいことから"fissile"、238Uはそのままでは核燃料になり得ないことから、"fissionable"と呼ぶ。図中に235Uの幾何学的断面積を示しているが、これは原子核を球体とみなしたとき、2次元に射影したときの円の面積である。これに、中性子が波の性質をもつという量子効果が加わって低エネルギーの中性子では断面積が大きくなっている。235Uと238Uの核分裂断面積の違いは、中性子数の偶奇性による性質の大きな違い(リンク先)からくるが、それだけではない。下記で説明を試みる。235Uと238Uの中性子核分裂反応のQ値(リンク先)を比較してみると、共におよそ200 MeV程度の発熱反応である。それにも関わらず、中性子核分裂断面積が大きくことなるのはなぜなのだろうか?また、どうして勝手に核分裂反応を発生させ、安定な2つの原子核になってしまわないのだろうか?ここに、核分裂障壁の存在のカギが隠されている。235Uと238Uの中性子結合エネルギーについて考える(図5)。今、これらのUに中性子が反応して、複合核(リンク先)を作る場合を考える。この場合、複合核は元の原子核より中性子1個分重い原子核である。235Uに中性子が衝突して236Uという複合核を作る際、中性子が持ち込むエネルギーは6.545 MeVである。236Uは235Uと中性子の重さを足したものより、結合エネルギーの分だけ軽くなるので、この差分が6.545 MeVという値と等しい。これは、のちに議論する核分裂障壁(5.3 MeV)より高い。このため、核分裂は壁を超えているので起りやすい。一方、238Uが中性子を吸収して239Uという複合核を作る際の中性子が持ち込むエネルギーは4.8061MeVであり、核分裂障壁(5.5 MeV)より低いので、核分裂するためには更に山を登らないといけない。他の原子核についての核分裂障壁と中性子結合エネルギーを表3に示す。核分裂障壁は、重い原子核ほど下がる傾向がある。
「235U+n→236U*→二つの核分裂片」の系を見てみよう(図6)。球形から僅かに歪んだ状態(回転楕円体)を考えると原子核の表面積が増加する。これは、表面近くの核子の繋がることのできる核子が減る(結合する核子が少ない核子数が増える)ことになり、全体的に原子核の結合エネルギー(核力)を小さくする効果、すなわち、原子核の質量エネルギーを増加させる効果をもたらす。このため、核分裂に向けて変形していくと、最初は内部エネルギーが増加(励起)する。一方、クーロン力のため、プラスの原子核同士は遠くにいるほど安定である。クーロン力しか無ければ、原子核は勝手に二つの核分裂片に分裂し、ウラン領域の原子核は存在できないことになる。
核力とクーロン力のどちらにより強く支配されるかは、変形する原子核の球形の時の半径(r)または回転楕円体の長い半径と短い半径の比(a/b)によって変化する。この関係を合わせて、核力からクーロン力への乗り替えの視点で考えてみる(図7)と核内では核力の方がクーロン力より大きいので、最初のうちは表面積の増加によるエネルギーの増加が主要となる。一方、分裂してしまえば核分裂片間のクーロン力(斥力)しか働かないので、最後はそのポテンシャルに乗り移る(Zが大きいほど強い斥力)。したがって、原子核が核分裂に向けて変形して行くときに感じるポテンシャルは図7の破線のようになり、途中に山ができる。これが、核分裂障壁である。実際には回転楕円体から二つの原子核に分かれる途中でヒョウタンのような中間的な形状も取るので、核分裂障壁は滑らかになる。核分裂障壁のおかげで、核分裂のQ値が正の原子核も存在できるのである。図8に核分裂障壁と原子核の典型的な変形を示す。基底状態から回転楕円体に近いときは体積( )の変化に従って、表面張力のつり合いによりエネルギーが変化する。核分裂後の核分裂片の運動エネルギーは、図8中Dのrcでのクーロンエネルギーにより決まる。
核分裂収率
235Uの中性子核分裂反応による核分裂片の分布を核図表上に表わすと図17のようになる。これを横軸に質量数、縦軸にその質量数を持つ核分裂片の分布を200%に規格化(2体核分裂と仮定した場合、1核分裂当たり2個の核分裂片が生成する)したものを示す(図18)。これを核分裂収率と呼ぶ。図の矢印はきれいに二つに割れた場合(対称核分裂)の質量数の位置(A=118近傍)を示す。これからわかるように核分裂収率は、非対称性が強い。元々の235Uが中性子の数が相対的に多い核種なので、核分裂生成物(Fission Product、FP)も図17の×印のβ安定核より下側の中性子過剰となり、主にβ-崩壊する放射性核種になる場合が多い。代表的なFP核種とその半減期は、90Sr(ストロンチウム、28.78 y)、137Cs(セシウム、30.07 y)、87Kr(1.27 h)、88Kr(2.84 h)、133Xe(キセノン、5.25 d)、135Xe(9.14 h)、129I(ヨウ素、1.57×107 y)などである。核分裂収率の特徴として、核分裂をする複合核の励起エネルギーとともに対称核分裂が増えることが挙げられる(図19)。また、図20に示すように、複合核が重くなっても重い核分裂片の分布はさほど変化せず、軽い核分裂片の山は質量数とともに重い方に動く。これは、図17でも示しているが、重い核分裂片の方はZ=50及びN=82(A=132)の二つの魔法数(リンク先)が含まれるため、非常に安定で、球形かつ硬い核分裂片が存在するため、軽い核分裂片の方が変化するためである。
核分裂収率を定量的に記述するために、2モード核分裂モデルが提唱された。これは、図8の分岐(シッション)点Dの変形ポテンシャルの微少な変化により、変形経路の大幅な変化が生じ、対称変形と非対称変形が起こると仮定する。しかし、このモデルの説明だけでは非常にシャープな分布しか記述できない。そこでいくつかのモデルが提唱されてきた。1959年にS.L.Whetstoneは、変形して伸びた複合核がくびれの中心を軸に正規分布に従い任意に断裂するとしたRandom Neck-Rupture Modelを提唱した(図22)。このモデルは核分裂中性子数ν(A)及び核分裂収率が広がりをもつことを定性的に説明可能としたが、単一の断裂前形状しか考えていないため定性的モデルにとどまることとなった。このため、断裂前形状をいくつか過程するマルチモード核分裂(図23)が導入され、核分裂収率の広がり及びν(A)の質量数Aに対する鋸歯状分布の説明等多くの事象を定量的に説明できるようになった。ここでは、断裂前の形状にSuper Long(対称核分裂)、Standard 1(質量数が近い非対称分裂)、Standard 2(質量数が離れている非対称分裂)を仮定している。近年、Standard 3(質量数が非常に離れている非対称分裂)を加えて237Np(ネプツニウム)の核分裂収率と運動エネルギー分布を説明した報告もある。
核分裂からの中性子放出
図24に核分裂における即発中性子放出過程を示す。標的核に中性子が入り、放出に十分な励起エネルギーを中性子が持っていれば核分裂反応以前の中性子(Pre-fission Neutron)放出が起る。これも核分裂中性子として考慮する。励起した複合核が断裂する前に中性子(Pre-scission Neutron)や複合核が十分に変形して断裂する時の中性子(Scission Neutron)を放出することもある。上述したが、核分裂片が十分な励起エネルギーを持っていれば、中性子を放出できるが、核分裂片加速時(Neutron Emission during Acceleration)または終速度に達した核分裂片(Neutron Emission after Full Acceleration)からの中性子放出と分けて考えることもでき、これによって中性子のエネルギースペクトルの実験室系での振る舞いをより正確に記述することができる。核分裂で生成した核分裂片は励起状態にあることが多い。この励起エネルギーが中性子分離エネルギー以上であれば中性子が放出される。放出される時間スケールは核反応の時間スケールで、およそ10-17秒までであるものを即発中性子という。後述する遅発中性子よりはずっと多く、核分裂中性子の大半は即発中性子である。核分裂で発生する平均中性子数(即発及び遅発中性子の総和)は図25のような入射中性子エネルギー依存性を持つ。この図ではほぼゼロエネルギー付近である熱中性子による核分裂中性子数は、235Uで平均として2.5個程度であり、重い原子核ほど多くなることが分かる。
核分裂生成物の一部はβ-崩壊に伴って中性子を放出する。β-崩壊でできた先の原子核の中性子分離エネルギーより高い励起状態ができた場合は中性子が放出される。この中性子を遅発中性子という。核分裂中性子の内、0.7%程度(235U+nの場合)。β-崩壊後に中性子を放出する核種を遅発中性子放出先行核(または先行核)といい、遅発中性子放出もこの先行核の崩壊にしたがって減少するが、原子炉運転中は 先行核が継続して作られるため、遅発中性子も継続的に存在する。先行核は多数あるが、半減期がもっとも長いのは87Br(臭素、55秒)である。87Brのβ崩壊による遅発中性子発生過程を図27に示す。β崩壊後の87Krの励起エネルギーが中性子を放出して86Krになるのに十分な大きさがあると、γ線遷移せずに中性子を放出する。この中性子は、87Brのβ崩壊の時間だけ遅れて放出されることとなる。遅発中性子の存在により、原子炉は即発中性子だけでは臨界にならないように制御することができ、急激な出力の変化を防ぐ時間的余裕が得られることになる。すなわち、遅発中性子なしには原子炉の臨界制御は困難であると言える。