第5章 光学模型 初級編
東京工業大学 片渕竜也
目次
1. はじめに
本章では核データの理論解析で重要となる光学模型について解説する。光学模型は、入射粒子の原子核による散乱を光の物質内での散乱と吸収のアナロジーとして捉えたモデルである。中性子や陽子の原子核との散乱現象を一体ポテンシャルによりよく説明することができる。光学模型で用いられる光学ポテンシャルの決定は核データの理論研究において重要な部分を占めている。2. 光学模型の導入

図1 中性子の全断面積を入射中性子エネルギーと標的原子核の質量数の関数
としてプロットした図文献2。Barschall曲面とも呼ばれる。断面積は幾何学的
断面積で規格化してある。
注目すべきは、その「大まかな構造」(gross structure)である。重要なポイントとして次の2点が挙げられる。
- 断面積のエネルギー依存性がエネルギーとともに緩やかに変化しており、このエネルギー依存性は質量数の近い隣り合った原子核ではよく似た形状となる。
- 質量数90付近の原子核は0.5 MeV以下の低エネルギー領域に断面積の極大値を持つが、質量数が大きくなるにつれて極大値は高エネルギー側にゆっくりとシフトする。質量数140付近に至ると断面積は1 MeVあたりに極大値を持ち、さらに重い原子核では極大値のエネルギーは3 MeVより大きくなり、その結果1 MeV付近の断面積は極小値となる。
共鳴理論が土台としているボーアの仮説では原子核内に入った入射中性子は直ちに複合核を形成する。原子核内では核子が強い相互作用の下で互いに頻繁に衝突しておりエネルギー交換が直ちに行われると考えたからである。しかし、高速中性子の全断面積のふるまいから原子核は中性子にとって意外と「透明」で中性子が原子核内に入っても直ちに複合核を形成するわけではなさそうだということが明らかとなった。
そこで、Feshbach, Porter, Weisskopfは、中性子の全断面積のふるまいを説明するために光学模型を提唱した文献4。光学模型では、光が透明な物質中を散乱・吸収を起こしながら伝播するように入射中性子は原子核中で振る舞う。彼らは、次のような井戸型の一体ポテンシャルを仮定し、中性子の全断面積を計算した。
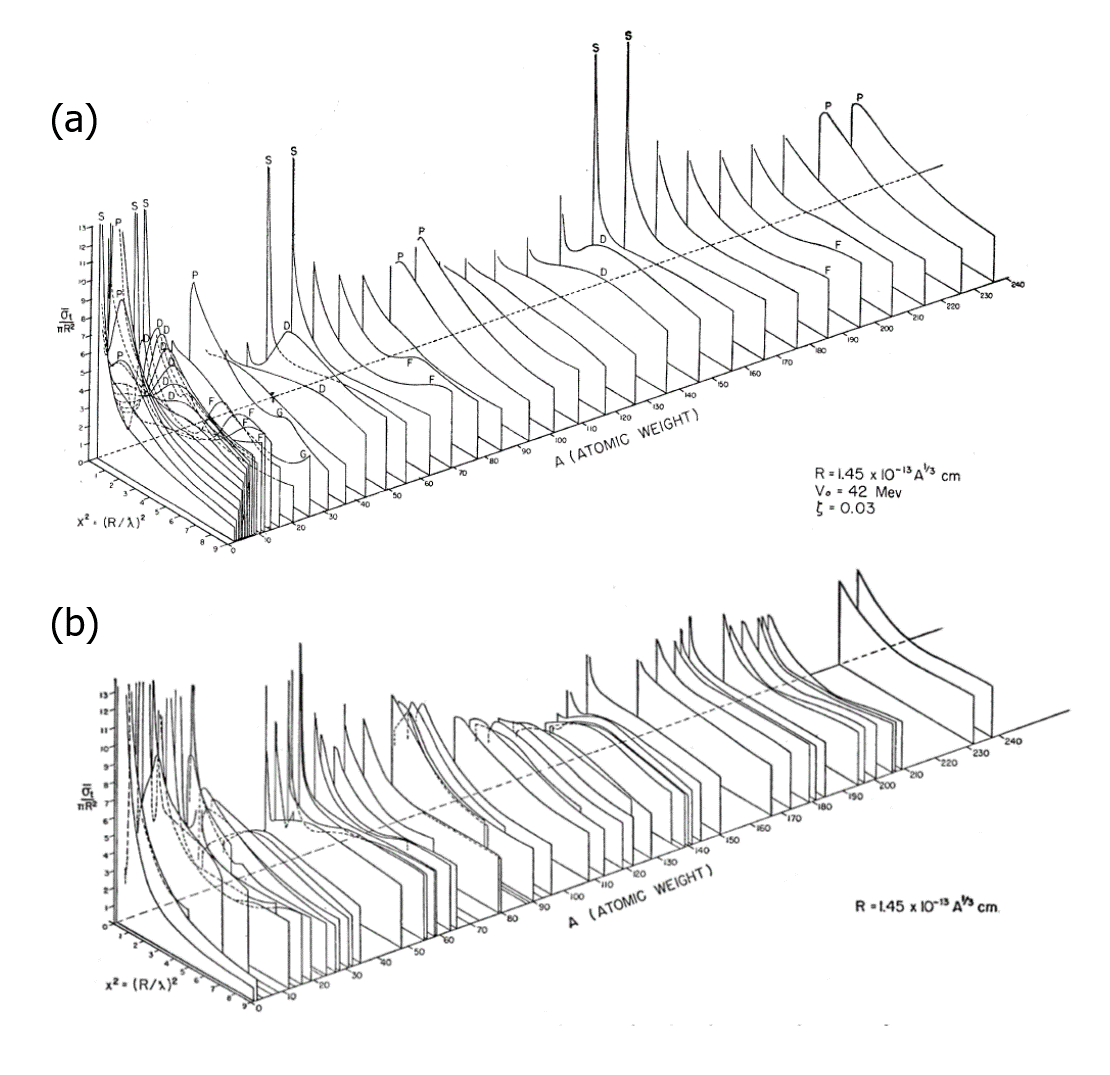
図2 (a) 式(5.1)の複素ポテンシャルを用いて計算された全断面積
(b) 図1の実験データを(a)と同様の形式でプロットした図文献4
Feshbachらの実際の計算では以下のようなポテンシャルパラメータが採用された。
\begin{align} R &= 1.45 \times 10^{13} A^{1/3}\: \mathrm{cm} \\ V_0 &= 42\: \mathrm{MeV} \\ \zeta &= 0.03 \tag{5.2} \end{align} 計算によって得られた全断面積を図2に示す。図1と同様に入射中性子エネルギーと標的原子核の質量数の関数としてプロットしている。図1に見られた「大まかな構造」を見事に再現できていることが分かる。
(平均自由行程)ここで光学模型を理解するために複素ポテンシャルの物理的意味をもう少し考えてみよう。
深さ\(U\)の井戸型ポテンシャル中の粒子の運動エネルギー\(p\)と波数\(k\)は、
\begin{align} p = \sqrt{2m(E+|U|)}, \:\: k = \frac{\sqrt{2m(E+|U|)}}{\hbar} \tag{5.3} \end{align} ここで\(E\)は粒子の入射エネルギー、\(m\)は質量である。ここで次のようにポテンシャルは虚数部を持つとする。
\begin{align} U = V+iW \tag{5.4} \end{align} 式(5.3)に代入すると波数\(k\)は \begin{align} k = \frac{\sqrt{2m(E+|V|+i|W|)}}{\hbar} \tag{5.5} \end{align} となる。式(5.2)にあるようにポテンシャルの虚数部は実数部に比べて小さいので波数\(k\)は近似的に以下のように書ける。
\begin{align} k \sim \frac{\sqrt{2m(E+|V|)}}{\hbar} + \frac{i}{\hbar} \sqrt{\frac{m}{2(E+|V|)}} |W| \tag{5.6} \end{align} ポテンシャルに虚数部のないときの波数を\(K\)、速さを\(v\)とすると
\begin{align} K &= \frac{\sqrt{2m(E+|V|)}}{\hbar} \tag{5.7}\\ v &= \frac{\hbar K}{m} = \sqrt{\frac{2(E+|V|)}{m}} \tag{5.8} \end{align} となるので、式(5.6)は
\begin{align} k \sim K + i \frac{|W|}{\hbar v} \tag{5.9} \end{align} と書ける。
波数\(k\)を持つ粒子の波動関数は、\(e^{ikz}\)なので式(5.9)を代入すると波動関数は
\begin{align} e^{ikz} &\sim e^{i(K + i \frac{|W|}{\hbar v})z} \\ &= e^{iKz} e^{-\frac{|W|}{\hbar v}z} \tag{5.10} \end{align} となる。入射粒子の密度分布\(\rho (z)\)は波動関数の絶対値の2乗なので
\begin{align} \rho (z) = |e^{ikz}|^2 \sim |e^{iKz} e^{-\frac{|W|}{\hbar v}z}|^2 = e^{-2\frac{|W|}{\hbar v}z} \tag{5.11} \end{align} となる。
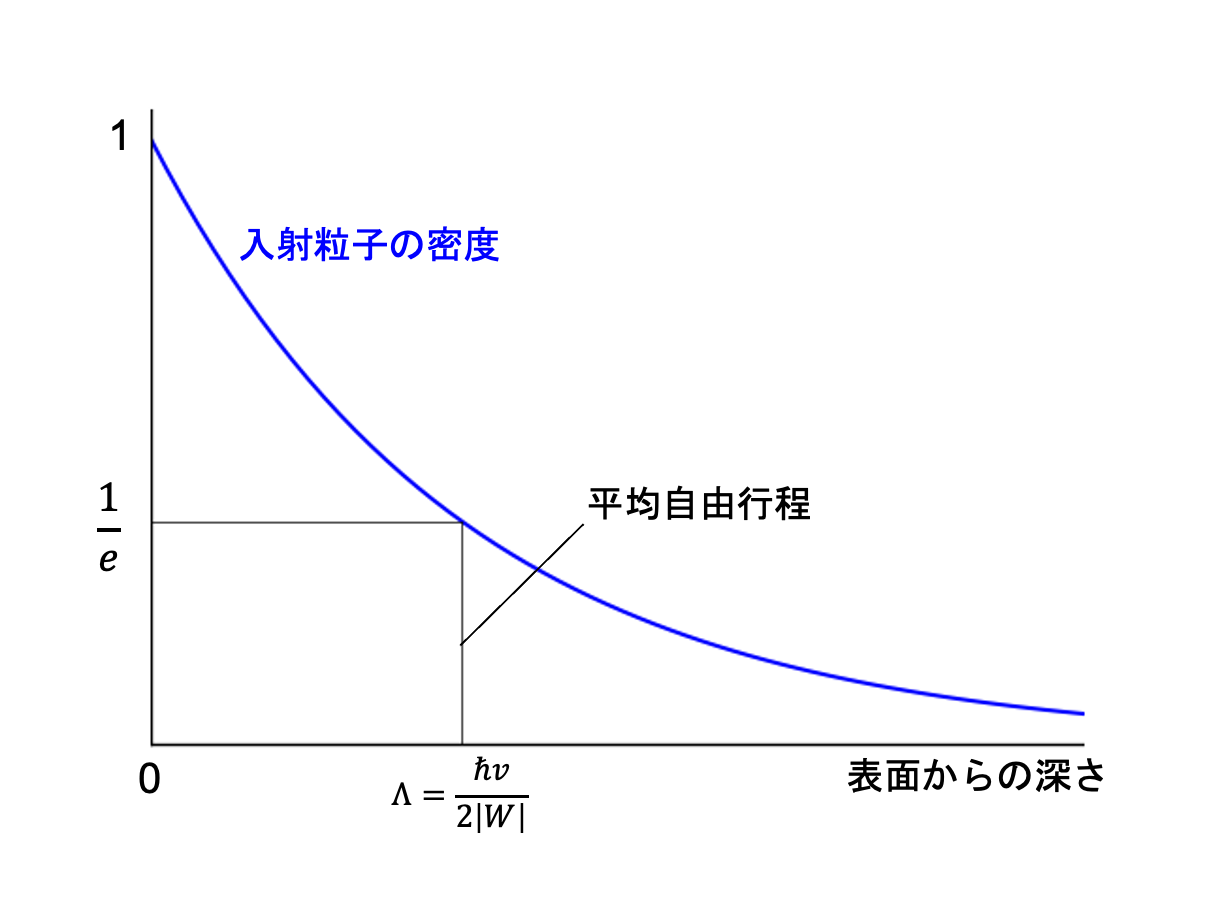
図3 平均自由行程
\begin{align} \Lambda = \frac{\hbar v}{2|W|} \tag{5.12} \end{align} である(ちなみに確率の流れの密度を用いれば、より厳密な議論が可能となる注2)。
(曇り水晶球模型)式(5.12)の平均自由行程がどれくらいの距離になるのか具体的な値を入れて計算してみよう。簡単のために中性子の入射エネルギーは非常に低くポテンシャルの深さに対して無視できるものとする(\(E=0\))。中性子の質量は、\(940\:\mathrm{MeV}\)とする。ポテンシャルパラメータとして(5.2)を採用し、\(V = 42 \:\mathrm{MeV}\)、\(W = 0.03 \times 42 \:\mathrm{MeV}\)とする。式(5.12)の\(v\)に式(5.8)を代入し、\(\hbar, m, V, W\)に具体的な値を代入すると平均自由行程は
\begin{align} \Lambda &= \frac{\hbar v}{2|W|} = \frac{\hbar}{2|W|} \sqrt{\frac{2 |V|}{m}} \\ &=\frac{\hbar c}{2|W|} \sqrt{\frac{2 |V|}{m c^2}} = \frac{197 \:\mathrm{MeV}\cdot\mathrm{fm}}{2\times0.03\times42\: \mathrm{MeV}} \sqrt{\frac{2\times42\:\mathrm{MeV}}{940\:\mathrm{MeV}}} = 23\:\mathrm{fm} \tag{5.13} \end{align}
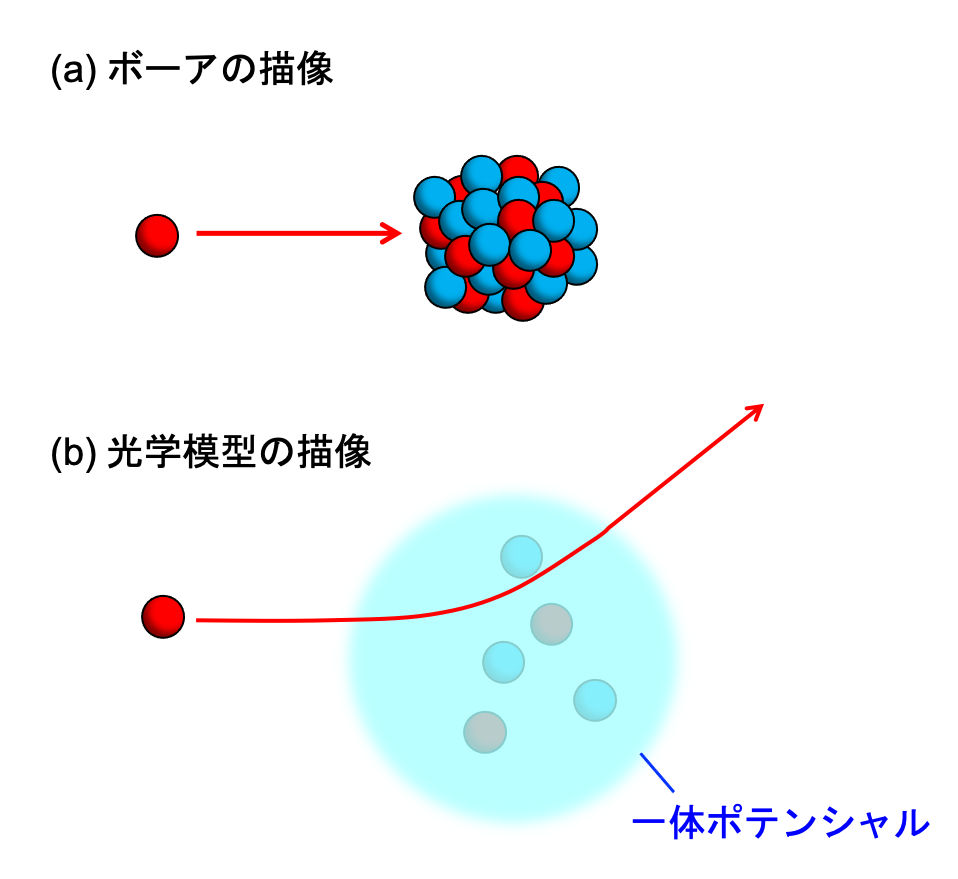
図4 ボーアの原子核の描像と光学模型の描像
原子核を曇り水晶球のようにとらえる考え方は一見直感に反しているように見える。原子核は核子が密に詰まった系であり、そこに入射した核子がほとんど反応を起こさずに通り抜けていくというのは信じがたいことである。ボーアは原子核中の核子は強い核力のもとで頻繁に衝突してエネルギーの交換をしており、原子中の電子のように一体ポテンシャル中を運動するという描像は成り立たないと考えた(図4(a))。これがボーアの複合核模型の土台になっている。ボーアの理論によれは原子核中に入り込んだ核子は直ちに原子核内の他の核子とエネルギー交換をし、全ての核子に入射エネルギーが分配される(平衡状態となる)。
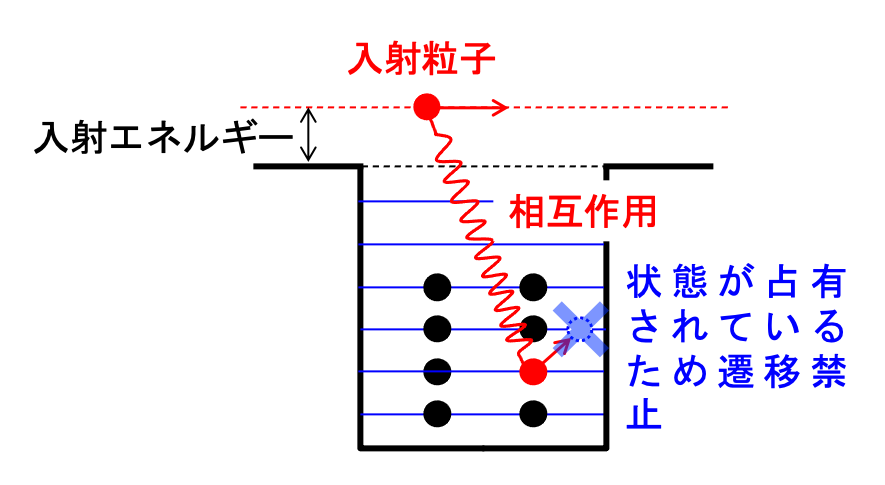
図5 入射粒子と核内核子の相互作用。
パウリの排他原理によりエネルギー
交換が強く制限される
3. 一体ポテンシャルによる散乱
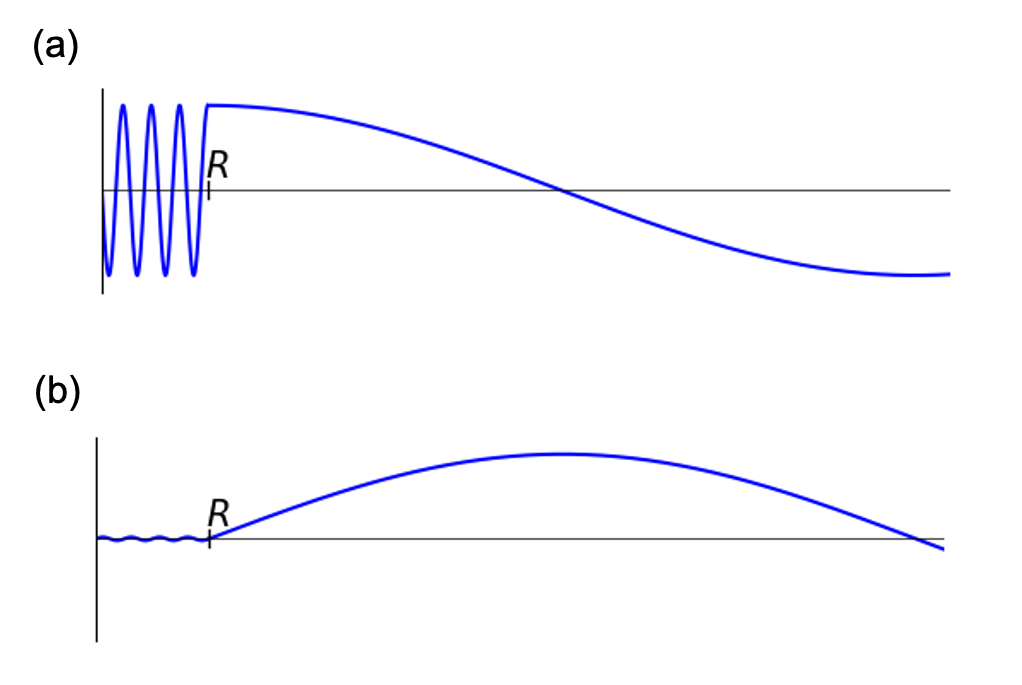
図6 式(5.15)の条件を(a)満たしたときと
(b)満たしていないときの波動関数
\begin{align} \sigma = 4\pi R^2 \left(1 - \frac{\tan K R}{K R}\right)^2 \tag{5.14} \end{align} この式から次のように\(K R\)が\(\frac{\pi}{2}\)の奇数倍になるときに断面積が極大値をとる。 \begin{align} K R &= \frac{\pi}{2}, \:\frac{3\pi}{2}, \:\frac{5\pi}{2} \ldots \\ &= \frac{\pi}{2} + n \pi ,\; (n =0, 1, 2, \ldots) \tag{5.15} \end{align} このとき内部波動関数\(u_{in}(r)\)は次の式で与えられる。
\begin{align} u_{in}(r) &= \frac{\sin K r}{K r} \tag{5.16}\\ \end{align}

図7 ポテンシャル半径の違いによる内部波動関数の
振幅の違い。半径がそれぞれ内部波動関数の波長の
(a) 1.75倍 (b) 2倍 (c) 2.25倍のとき
以上の結果が図1の断面積の振る舞いとどのように関係するのか見てみよう。\(K R\)は式(3.70)より
\begin{align} K R = \frac{\sqrt{2 m (E + V_0)}}{\hbar} R \tag{5.17} \end{align} である。今、低エネルギーの入射を考えているので\(E = 0\)とすると、式(5.15)の条件は
\begin{align} \frac{\sqrt{2 m V_0}}{\hbar} R = \frac{\pi}{2} + n \pi ,\; (n = 0, 1, 2, \ldots) \tag{5.18} \end{align} となる。ポテンシャルの深さは変化しないので、(5.18)の条件は原子核半径\(R\)のみに依存していることが分かる。つまり原子核の半径がちょうど(5.18)の共鳴条件を満たしたときに断面積は大きくなる(図7)。実際、図1および図2の低エネルギー領域の断面積は質量数が50付近と160付近で大きくなっているが、これはまさに原子核半径がちょうどs波の形状共鳴条件を満たしたために生じたものである。
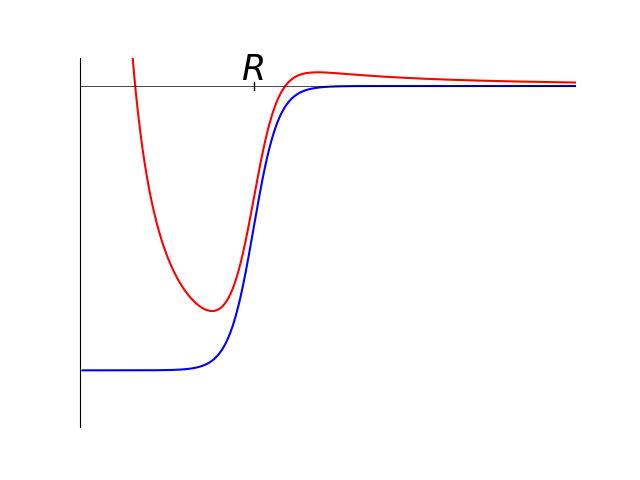
図8 遠心力がある場合(赤)とない場合(青)のポテンシャル
ちなみに図1で質量数140付近の断面積が1 MeV付近で大きくなっているのは、図2の計算結果でDと書かれているように\(l = 2\)のd波の形状共鳴によるものである。
4. 形状共鳴と複合核共鳴
ここで4章で述べた複合核共鳴と形状共鳴の関係について述べておこう。5. 光学ポテンシャルの精密化

図9 ウッズ-サクソンポテンシャル
\begin{align} f(r, R, a) = \frac{1}{1+\exp\left[(r-R)/a\right]} \tag{5.19} \end{align} \(R\)は核半径、\(a\)は、ぼやけのパラメータ(diffuseness parameter)と呼ばれる。
また、中心力だけでなくスピン軌道相互作用も導入される。スピン軌道相互作用は原子核の殻模型において重要な役割を果たした。同様に核反応においても重要な部分を担う。スピン軌道相互作用は、入射核子の軌道角運動量を\(\boldsymbol{l}\)、入射核子スピンを\(\boldsymbol{s}\)とするとその内積 \begin{align} \boldsymbol{l}\cdot\boldsymbol{s} \tag{5.20} \end{align} に比例する力である。式から分かるように\(\boldsymbol{l}\)と\(\boldsymbol{s}\)の方向が平行か反平行かにより力の符号が変わる。
光学ポテンシャルの具体的な形としてウッズ-サクソンポテンシャルを用いた以下の形のポテンシャルがよく採用されている文献5。入射エネルギが200 MeV以下でよく実験値を再現する。
\begin{align} V(\boldsymbol{r}) = -V_r f(r, R_0, a_0) - iW_v f(r, R_w, a_w) - iW_s (-4 a_w )\frac{d}{dr}f(r, R_w, a_w) &\\ -2 (V_{SO} + iW_{SO})\left(\frac{-1}{r}\frac{d}{dr}f(r, R_{SO}, a_{SO})\boldsymbol{l}\cdot\boldsymbol{s}\right)+V_C & \tag{5.21} \end{align} 1項目の\(V_r f(r, R_0, a_0)\)は中心力ポテンシャルの実数部である。
2項目と3項目は中心力ポテンシャルの虚数部であり、体積項\(iW_v f(r, R_w, a_w)\)と表面項\(iW_s (-4 a_w )\frac{d}{dr}f(r, R_w, a_w)\)からなる。表面項は原子核表面で働く力であり、そのためウッズ-サクソンポテンシャルの微分形が含まれている。図9から微分係数が表面付近で大きくなることが分かるだろう。原子核内部に比べ外側の核子はパウリの排他原理の効果が弱い。そのため吸収項である虚数ポテンシャルの強さが内部と表面で異なると考えられることから体積項と表面項が導入されている。
4項目はスピン軌道相互作用である。スピン軌道相互作用も実部と虚部を持つことから\(V_{SO}\)と\(iW_{SO}\)が導入されている。スピン軌道相互作用にもウッズ-サクソンポテンシャルの微分形が含まれているが、これは原子物理における電子のスピン軌道相互作用のアナロジーからこの形が採用されている注6。
最後の項\(V_C\)はクーロンポテンシャルである。中性子の場合には当然ゼロである。陽子の場合には一様に帯電した球のポテンシャルが用いられる。すなわち
\begin{align} V_C(r) = \left\{ \begin{array}{ll} \frac{Z e^2}{r} & (r \geq R_C) \tag{5.22}\\ \frac{Ze^2}{2 R_C}\left(3 - \frac{r^2}{R_C^2}\right) & (r \lt R_C) \end{array} \right. \end{align}
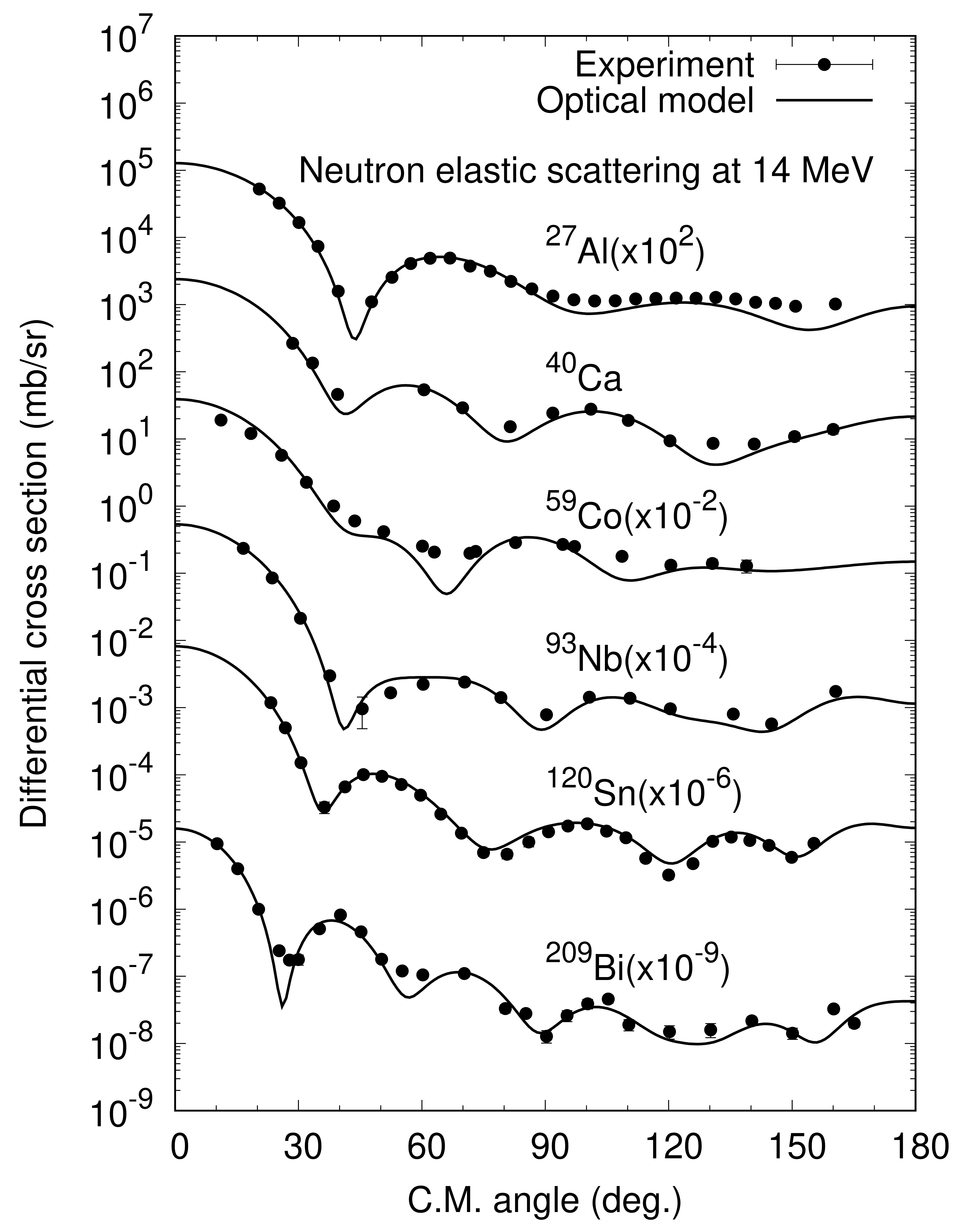
図10 14 MeV中性子の弾性散乱微分断面積に対する
光学模型によるフィッティング(JAEA 中山梓介氏提供)
式(5.21)と式(5.22)に現れる12個の係数\(V_r,\) \( R_0,\) \( a_0,\) \( W_v,\) \( R_w,\) \( a_w,\) \( W_s,\) \( V_{SO},\) \( W_{SO},\) \( R_{SO},\) \( a_{SO},\) \( R_C\)は光学ポテンシャルを決めるパラメータである。これらの光学ポテンシャルパラメータは、図1に示したような全断面積に加えて、弾性散乱の微分断面積の角分布、偏極分解能注7といった実験値を再現するように決定される。一例を図10に示す。
光学ポテンシャルパラメータは個々の散乱実験のデータセットごとにフィッティングが最適になるように決定することもできるが、そのように決定されたパラメータはあくまでその実験条件の場合にしか適用できないことからあまり実用的ではない。むしろパラメータが、入射エネルギー\(E\)、標的原子核の陽子数\(Z\)、中性子数\(N\)に対し緩やかに変化する関数と考え、多くの実験値に対して全体的によく再現するパラメータを求めるほうが実用的である。これを広域光学ポテンシャル(global optical pontential)と呼ぶ。広域光学ポテンシャルを用いることで実験値の存在しない入射エネルギーや標的核について断面積を求めることができ、断面積の核データ評価値を整備する上で有用である。したがって、広く収集した測定値に基づき信頼性の高い広域光学ポテンシャルを決定することは核データ研究の重要なタスクのひとつとなっている。現在広く用いられている中性子と陽子の広域光学ポテンシャルとして、KoningとDelarocheのポテンシャル文献6や国枝らのポテンシャル文献7が挙げられる。
注釈
- \(r = 1.45\times A^{\frac{1}{3}}\)としている。
-
\begin{align}
U(\boldsymbol{r}) = V(\boldsymbol{r}) + iW(\boldsymbol{r})
\end{align}
\begin{align}
i\hbar\frac{\partial \Psi(\boldsymbol{r},t)}{\partial t} &= \left(-\frac{\hbar^2}{2m}\nabla^2 + V(\boldsymbol{r}) + iW(\boldsymbol{r}) \right)\Psi(\boldsymbol{r},t) \tag{5.3}
\end{align}
ここで密度\(\rho\)および流れの密度\(\boldsymbol{j}\)を次のように定義する。
\begin{align} \rho &= \Psi^* \Psi \tag{5.4} \\ \boldsymbol{j} &= \frac{\hbar}{2 i m}\left(\Psi^* \nabla \Psi - \Psi \nabla \Psi^*\right) \tag{5.5} \end{align} 式(5.3)の左から\(\Psi^* \)を掛け虚数部を取り出すと
\begin{align} \nabla \cdot \boldsymbol{j}(\boldsymbol{r},t) +\frac{\partial }{\partial t} \rho(\boldsymbol{r},t) = \frac{2}{\hbar}W(\boldsymbol{r})\rho(\boldsymbol{r},t) \end{align} \begin{align} \frac{v}{\Lambda} = \frac{2}{\hbar}|W(\boldsymbol{r})|\\ \therefore \Lambda = \frac{\hbar v}{2 |W(\boldsymbol{r})|} \end{align} - 現在採用されている光学ポテンシャルの虚数項は(5.2)より3倍程度大きい。したがって、平均自由行程は7 fm程度になる。したがって、入射中性子は原子核内で1回程度の反応を起こすという結論により近くなる。ここでは本質的な議論には影響を与えないので簡単のために(5.2)のパラメータを用いた。
-
原子核半径の経験公式に質量数150を代入すると
\begin{align}
r = 1.45\times A^{\frac{1}{3}} = 1.45\times 150^{\frac{1}{3}} =7.4\:\mathrm{fm}
\end{align}
となる。
-
より現実的な状況を図示するために井戸型ポテンシャルではなく後述するウッズ-サクソンポテンシャルに遠心力ポテンシャルを足し合わせた。図では境界付近のポテンシャルが正側に少し盛り上がっているだけのように見えるがポテンシャル深さが50 MeVくらいあることを考えれば、この障壁は意外と大きい。
-
スピン軌道相互作用
-
偏極分解能(analyzing power)
参考文献
- D. W. Miller et al., Physical Review 88, 83 (1952).
- H. H. Barschall, Physical Review 86, 431 (1952).
- H. Feshbach and V. F. Weisskopf, Physical Review 76, 1550 (1949).
- H. Feshbach, C. E. Porter and V. F. Weisskopf, Physical Review 96, 448 (1954).
- R. L. Varner et al., Physics Reports 201, 57 (1991).
- A. J. Koning and J. P. Delaroche, Nuclear Physics A 713, 231 (2003).
- S. Kunieda et al, Journal of Nuclear Science and Technology 44, 838 (2007).