第1章 量子力学の基礎 初級編
東京工業大学 片渕竜也
目次
1. はじめに
原子のサイズは、10\(^{-10}\) m程度と小さい。さらに原子核は、原子よりもさらに4桁も5桁も小さい。したがって、核データが扱う原子核が関わる現象の理解には微視的世界を記述する量子力学の知識が多少なりとも必要である。当初、この核データの教科書を書くにあたって量子力学そのものについては多くの教科書が存在するため、記述の必要はないと考えていた。また、初級編ではなるべく量子力学には触れずに書こうと考えていた。しかし、それは無謀な試みであることを強く認識した。最初に最低限必要な量子力学の知識を与えた方が初学者の理解にはよいとの結論に至った。したがって、この章では核データを理解する上で必要な量子力学のエッセンスを伝える。さらに本格的で精緻な理論を学びたい読者は、専門的な教科書で勉強してほしい。量子力学は誰か一人の理論家が作り上げた理論体系ではない。19世紀末から20世紀初頭にかけて次々と発見された微視的世界の驚嘆の実験事実注1を説明するために多くの物理学者が試行錯誤の末に作り上げたものである。したがって、入門としては、理論的枠組だけではなく歴史的な経緯、実験事実に触れながら解説するほうが理解の助けになると考えた。そのため少し冗長になったが、その点ご容赦願いたい。
2. 物質の波動性
量子力学を特徴づける最も重要なポイントは、波動性と確率である。物質の波動性は、ド・ブロイによってはじめて示唆されたが、それに触れる前に光の理解についての歴史的な話から始める。17,18世紀の光の干渉現象の研究から光は波であるとの理解が深まった。しかし、その波動の実体が何なのかは分からなかった。19世紀になるとマクスウェルが電磁気学を完成し、マクスウェル方程式から空間を伝播する電磁波の存在を予言した。そして、マクスウェルの天才的な推論により、可視光(すなわち光)もまた電磁波の一種であることが示された。これで光の理論は完成されたかに見えた。しかし、20世紀初頭、光を粒子と仮定しないと説明がつかない現象が次々と発見されることとなる注2。その最も単純で分かりやすい例が光電効果である。光電効果は、物質に光を当てるとその表面から電子が飛び出してくる現象である文献1。この現象には次の特筆すべき点がある。
- 光電効果を起こす光の振動数にしきい値があり、ある振動数以下になると電子が飛び出してこなくなる。しきい振動数以下ではいくら光の強度を増しても電子は出てこない。
- 振動数を増やすと電子の運動エネルギーは大きくなるが、飛び出してくる電子の数は変わらない。
- 光の強度を強くすると飛び出す電子の数が増えるが、電子1個あたりの運動エネルギーは変わらない。
結局、この問題はアインシュタインが光量子仮説を導入することで解決された文献2。すなわち、光は粒子から構成され(この粒子を光子と呼ぶ)、光電効果により1個の光子が吸収され1個の電子が放出される。光の振動数を\(\nu\)とした時、1個の光子の運動エネルギー\(E\)が振動数\(\nu\)に比例し、 \begin{align} E &= h\nu \tag{1.1} \end{align} であると仮定すれば、光電効果により放出される電子の運動エネルギー\(T\)は次の式で表される。
\begin{align} T &= E - W = h\nu - W \tag{1.2} \end{align} ここで比例係数\(h\)はプランク定数と呼ばれる。また、\(W\)は光電効果を起こすのに必要なエネルギー(仕事関数と呼ばれる)である。
以上の仮定により、それまで説明が困難だと思われた光電効果は、光子という概念を取り入れることで、非常に明快に説明された。
一方、光の粒子性を示すもう一つの現象であるコンプトン散乱の研究文献3から、光の波長を\(\lambda\)とすると光子の運動量\(p\)は
\begin{align} p &= \frac{h}{\lambda} \tag{1.3} \end{align} となることが分かった。
以上のことから、光は波動でもあり粒子でもあるという一見相矛盾する2つの性質をあわせ持つことが判明した。
式(1.1),(1.3)は、重要な帰結なのでここにまとめておく。また、プランク定数は、\(\hbar=\frac{h}{2\pi}\)が用いられることが多いので、\(\hbar\)を用いた表式も記した。
\begin{align}
E &= h\nu = \hbar\omega \tag{1.4} \\
p &= \frac{h}{\lambda} = \hbar k \tag{1.5}
\end{align}
ここで、\(\omega\)は角周波数、\(k\)は波数で次のように定義される
\begin{align}
\omega = 2\pi \nu, \hspace{1cm} k = \frac{2\pi}{\lambda}
\end{align}
(ド・ブロイの物質波)光の粒子性の理解が進む一方で物質もまた粒子から構成されることが観測事実から明らかとなった注3。具体的には、電子の発見、原子核の発見、陽子の発見と次々に物質を構成する粒子が発見された。このような中でフランスの物理学者、ド・ブロイはさらに進んだ仮説を提唱した。ド・ブロイは、自身の博士論文の中で光が波動と粒子の両面の性質を持つのであれば、逆に全ての物質粒子もまた波動としての性質を持つのではないかと提起した(この波動は物質波と呼ばれる)文献4。そして、物質粒子が運動量\(p\)を持つとすれば、その物質波の波長\(\lambda\)は式(1.5)と全く同じ形で結び付けられるとした。すなわち\begin{align} p &= \frac{h}{\lambda} \tag{1.6} \end{align} という関係が成り立つ。

図1 デヴィッスンとガーマーの実験
電子ビームを用いた回折実験から分かったことをまとめると次のようになる。
- 1個の電子は空間の1点で観測される。多数回の観測を繰り返すと電子の検出点の分布が回折模様となって現れる
- 観測される回折縞の間隔は、電子が空間的に広がった波動であるとするとよく説明がつく。
- 電子ビームの強度を弱めて電子が1個ずつしかニッケル結晶に当たらないようにしても回折模様は現れる。すなわち複数の電子が干渉しあって生じた結果ではない。
3. 波動と確率

図2 電子の二重スリット実験
図2に示すように電子銃から出た電子を2つの孔の空いたスリットを通した後、検出スクリーンで電子を検出する注4。電子が検出スクリーンに当たるとその位置が記録される。電子銃からの電子線の強度は弱く、電子は1個ずつスリットを通過し検出スクリーンに当たるとする。つまり、複数の電子が同時にスリットを通り検出されることはないものとする。したがって、電子はスクリーン上の1点で検出される。測定のたびに検出位置はばらつく。測定を多数回繰り返すと電子の検出位置はある確率分布を持ってばらつくことが分かる。検出点の密度から確率分布が得られる。
まず、片方の孔をふさいで1個のスリットで実験をやってみよう。例えば、孔1だけ空けて実験する。すると、スクリーン上で観測される電子の確率分布は図2(a)の\(P_1\)のようになる。孔1の射影位置の検出確率が一番大きくてそこから離れるに従って徐々に小さくなっていく。自然な分布である。今度は孔2だけ空けて実験をやってみよう。孔2は中心軸に対して孔1と対称な位置にある。したがって、得られる測定結果は当然のことながら\(P_1\)を中心軸に対して反転させたものになるだろう。この分布を\(P_2\)とする。
では、両方のスリットを空けた実験をやるとどうなるだろうか。常識的に考えれば、1個の電子は孔1か孔2のどちらか一方の孔を通過するはずなので検出スクリーン上の確率分布は片方の孔だけでやったときのそれぞれの確率分布\(P_1, P_2\)の和になるはずである。すなわち、\(P_1+P_2\)である。しかし、実際に観測される分布\(P_{12}\)はそうはならないのである。
\begin{align} P_{12} &\neq P_1+P_2 \\ \end{align} 実際に観測される分布は図2(c)に示すような山と谷を繰り返す不思議な構造を示す。なぜ、このようなことが起きるのであろうか。それは、\(P_1+P_2\)が成り立つための前提条件「1個の電子は孔1か孔2のどちらか一方の孔を通過するはず」が誤っているからである。ニュートン力学的に電子の運動が記述されるのであれば、観測していようがいまいが、電子はある軌道にしたがって運動する。軌道に沿って時刻毎の電子の位置と運動量が与えられる。電子はどちらか一方の孔しか通過しない。
しかし、自然はそうはなっていなかった。実験から明らかになったことは、ミクロな粒子の運動はニュートン力学では記述できないことであった。ニュートン力学で扱われる各時刻の正確な位置と運動量はもはや意味をなさない。代わりに観測されていない時の電子の振る舞いは波動関数という複素数の波で記述される。検出スクリーン上の波動関数の振幅を\(\psi\)とすれば、検出スクリーン上の検出確率はその絶対値の2乗\(|\psi|^2\)で与えられることが分かった。孔1だけのときの振幅を\(\psi_1\)、孔2だけのとき振幅を\(\psi_2\)とすれば、\(P_1, P_2\)は次のようになる。 \begin{align} P_1 &= |\psi_1|^2 \\ P_2 &= |\psi_2|^2 \end{align}
さらに両方の孔を空けたときに観測される不思議な繰り返しパターンはは干渉縞であることが説明される。両方の孔を空けたときの確率振幅は2つの波の和\(\psi_1+\psi_2\)であり、この波の重ね合わせにより干渉が生じ縞状のパターンが生じる。検出確率\(P_{12}\)は波動関数の振幅の絶対値の2乗で与えられるので \begin{align} P_{12} &= |\psi_1+\psi_2|^2 \tag{1.7}\\ \end{align} となる。理解のためにこの式をもう少し展開してみると次のようになる。
\begin{align} P_{12} &= |\psi_1+\psi_2|^2 = (\psi_1+\psi_2)^*(\psi_1+\psi_2)\\ &= \psi_1^*\psi_1+ \psi_1^*\psi_2+\psi_2^*\psi_1+\psi_2^*\psi_2\\ &= |\psi_1|^2+|\psi_2|^2+ \psi_1^*\psi_2+\psi_2^*\psi_1\\ &= P_1 + P_2 + \psi_1^*\psi_2+\psi_2^*\psi_1 \tag{1.8} \end{align} \(P_1+P_2\)に\(\psi_1^*\psi_2+\psi_2^*\psi_1\)が加わっている。この項が干渉項である。
以上、これが物理学者が辿りついた電子の波動性の正体であるが、そもそもこの波動関数とは何なのだろうか。まず、波動関数は観測可能な実体はない。例えば、音波であれば空気の疎密波だし、電磁波であれば電場や磁場の波である。観測可能な物理的実体のある波である。しかし、波動関数は観測可能な波ではない。では、存在するのか。哲学的な問いだが、そもそも観測できないものに対し「存在」を問うこと自体が意味をなさないというのが量子力学の見解である。また、観測できないがゆえに波動関数の振幅を複素数で記述しても差し支えない注5。逆に波動関数は複素数で記述しないと量子力学は成り立たない。つまり、複素数で表現され観測もできない、この幽霊のような波動関数という波によって電子の振る舞いは支配されているのである。

図3 2つの波の干渉
量子力学の難しさは、ここにある。量子力学は、我々が日常の経験から積み上げた直感に反する。であるがゆえに受け入れることに抵抗がある。しかし、これは我々のマクロな世界の常識がミクロな世界に通用しないということに過ぎない。常識に反しているということを除けば、実際にはルールは驚くほど簡単である。一番の早道はそれに慣れることである。
4. 量子力学の考え方
(演算子と固有値方程式)量子力学では、演算子と固有値方程式が数学的土台となっているので、まず、それらについて説明する。演算子とは任意の関数に作用して他の関数に変えてしまう数学的要素である。演算子であることを示すためにしばしば\(\hat{A}\)のように文字の上にハット記号 \(\hat{ }\) を付ける。
例えば、\(x\)の関数\(\psi(x)\)に作用する一番簡単な演算子として\(\hat{A}=x\)が考えられる。\(\psi(x)\)に\(x\)を乗ずる演算子である。つまり、
\begin{align} \hat{A} \psi(x) &= x \psi(x) \end{align} である。
また、微分演算子\(\partial/\partial x\)の関数を演算子\(\hat{A}\)とすることも可能である。例えば、
\begin{align} \hat{A} = \frac{\partial^2}{\partial x^2} \end{align} とすると \begin{align} \hat{A} \psi(x) = \frac{\partial^2 \psi(x)}{\partial x^2} \end{align} である。
演算子\(\hat{A}\)に対し、一組の数\(a_n\)と一組の関数\(u_n(x)\)が存在して方程式 \begin{align} \hat{A} u_n(x) = a_n u_n (x) \tag{1.9} \end{align} をみたすとき、\(a_n\)を固有値、\(u_n(x)\)を固有関数という。また、式(1.9)を演算子\(\hat{A}\)の固有値方程式という。
(交換関係)2つの演算子\(\hat{A}, \hat{B}\)を連続して関数に作用させるとき、その順番が重要になる。初めに\(\hat{B}\)を作用させた後、\(\hat{A}\)を作用させて得られた結果と、\(\hat{A}\)を作用させた後、\(\hat{B}\)を作用させて得られた結果が一致するとは限らない。例えば
\begin{align} \hat{A} =x, \;\hat{B} = \partial/\partial x \tag{1.10} \end{align} とすると
\begin{align} \hat{A}\hat{B} \psi(x) &= x\frac{\partial \psi(x)}{\partial x}\\ \hat{B}\hat{A} \psi(x) &= \frac{\partial x\psi(x)}{\partial x}=\psi(x)+x\frac{\partial \psi(x)}{\partial x} \end{align} となり、\(\hat{A}\hat{B}\)と\(\hat{B}\hat{A}\)の結果が異なることが分かる。
2つの演算子の順番を変えて得られた結果の差の演算子を交換子といい次のように定義される。
\begin{align} [\hat{A},\hat{B}] = \hat{A}\hat{B}-\hat{B}\hat{A} \tag{1.11} \end{align} 式(1.10)の例\(\hat{A}=x, \; \hat{B} = \partial/\partial x\)で交換子を作り関数に作用させると
\begin{align} [\hat{A},\hat{B}] \psi(x) &= (\hat{A}\hat{B}-\hat{B}\hat{A})\psi(x)\\ &= (x\frac{\partial}{\partial x}-\frac{\partial}{\partial x}x)\psi(x)\\ &= x\frac{\partial \psi(x)}{\partial x}-\psi(x)-x\frac{\partial \psi(x)}{\partial x}\\ &= -\psi(x) \end{align} この結果は任意の関数について成り立つので次のように書くことができる。
\begin{align} [\hat{A},\hat{B}] &= -1 \tag{1.12} \end{align} このような2つの演算子の交換子を決める方程式を交換関係という。
(演算子と観測操作)量子力学において観測という操作は本質的に重要な意味を持っている。古典力学においては、観測操作は対象としている系に対する影響を極力小さくし、系の状態を乱すことなく正確な全ての物理量を知ることは原理的に可能だとされている。しかし、量子力学では観測操作は系の状態に不可避的に影響を与える。例えば、上で取り扱った二重スリット実験で言えば、電子がどちらかの孔を通ったのか観測する操作を行うとスクリーン上の干渉縞は消えてしまう。したがって、観測操作は量子力学において本質的なものであり、理論的な枠組みの中に組み込まれている。
観測操作がもつ主要な性質として次の2つが挙げられる。
- ある系に対する観測(例えば、位置、運動量、エネルギーなどの物理量の測定)により得られる測定値の組は古典物理学のように連続的な範囲を取ることもあるし、水素原子のエネルギー準位のように離散的な値の集まりになることもある。
- 2つの観測操作があったとき、その観測操作の順序によって得られる観測結果は異なる。
以上のことを定式化し次のような規則を導入する。
- ある観測\(\hat{A}\)を行って得られる測定値は、この演算子のどれかの固有値\(a_n\)である。
- 系が固有状態\(u_n(x)\)にあるとき、観測\(\hat{A}\)を行って得られる測定値は、確実に固有値\(a_n\)である。
- 状態\(\psi(x)\)にある系をたくさん用意し注6、その各々に対し観測\(\hat{A}\)を行ったときの測定値の平均\(\langle a\rangle\)は次式で与えられる注7。 \begin{align} \langle a\rangle = \frac{\int\psi^*(x)\hat{A}\psi(x)dx}{\int\psi^*(x)\psi(x)dx} \tag{1.13} \end{align}
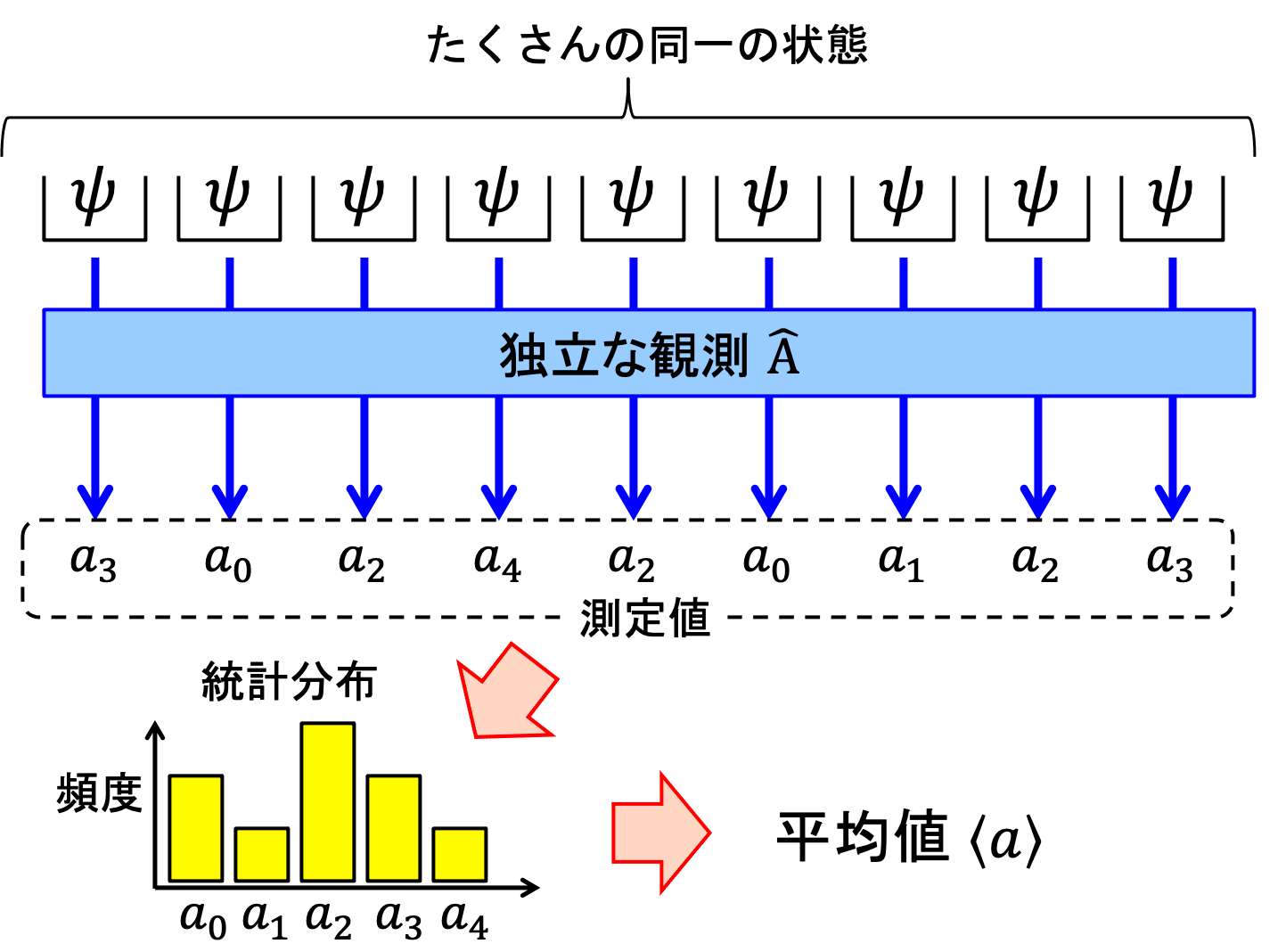
図4 観測と統計分布
規則3は少し難しいことを述べている。一般的な状態(つまり固有状態とは限らない)の系に対して観測\(\hat{A}\)を行う。このとき、1回の観測で得られる測定値は複数の固有値のうちどれか一つだが、たくさんの同一な状態の系に対して独立な観測を行うと測定値すなわち演算子\(\hat{A}\)の固有値の統計的な分布が得られる(図4)。規則3はこの統計分布から得られる測定値の平均値は式(1.13)で与えられることを述べている。この式については、また9節で取り扱うが、ここでは特別な場合、すなわち\(\psi(x)\)が固有状態\(u_n(x)\)である場合について見てみよう。
式(1.13)で
\begin{align} \psi(x) = u_n(x) \end{align} とすると、
\begin{align} \frac{\int u_n^*(x)\hat{A} u_n(x) dx}{\int u_n^*(x) u_n(x)dx} = \frac{\int u_n^*(x) a_n u_n(x) dx}{\int u_n^*(x) u_n(x)dx} = a_n\frac{\int u_n^*(x) u_n(x) dx}{\int u_n^*(x) u_n(x)dx} = a_n \tag{1.14} \end{align} となり、固有状態の場合には、その測定値の平均は固有値になるということを意味している。すなわち規則2と矛盾しない結果が得られた。
5. 位置と運動量の演算子
前節までは、やや抽象的な議論だったが、ここからは演算子をより具体的なものとして議論をすすめる。まず、位置の観測\(\hat{x}\)と運動量\(\hat{p}\)の観測に対応する演算子を次のように定める注8。
\begin{align} \hat{x} &\rightarrow x \tag{1.15}\\ \hat{p} &\rightarrow -i\hbar\frac{\partial}{\partial x} \tag{1.16} \end{align} この演算子のとり方をシュレーディンガーの表現と呼び、最もよく知られている位置と運動量の演算子表現である。
演算子\(\hat{p}\)の表現を\(-i\hbar\frac{\partial}{\partial x}\)とする理由だが、これは\(\hat{p}\)の固有状態を考えるとよく分かる。運動量演算子の固有状態とは、すなわち一定の運動量を持つ粒子である。演算子\(\hat{p}(=-i\hbar\frac{\partial}{\partial x})\)に対する固有値方程式は
\begin{align} -i\hbar\frac{\partial u(x)}{\partial x} &= p u(x) \tag{1.17} \end{align} である。ここで\(u(x)\)は固有関数、\(p\)は固有値である。運動量\(p\)を持つ粒子の状態である。
式(1.17)を解くと
\begin{align} u(x)= \exp(i\frac{p}{\hbar}x) \tag{1.18} \end{align} が得られ、固有関数は空間的に周期的に繰り返す波動となることが分かる(振幅は議論を簡単にするために\(1\)とした)。この固有関数の波長\(\lambda\)は
\begin{align} \lambda = \frac{2\pi\hbar}{p} =\frac{h}{p} \end{align} となり、これはド・ブロイ波の波長に他ならない。つまり、\(\hat{p}=-i\hbar\frac{\partial}{\partial x}\)とすることでド・ブロイの物質波が自然な形で導き出せるのである。
(不確定性原理)量子力学では位置と運動量を同時に正確に決定することができない。これは有名なハイゼンベルクの不確定性原理として知られている。また、その不確定性の度合はプランク定数程度になる。
不確定性原理は交換関係という形でうまく理論に組み込まれている。位置と運動量演算子の交換関係は
\begin{align} [\hat{x},\hat{p}] \psi(x) &= (\hat{x}\hat{p}-\hat{p}\hat{x})\psi(x)\\ &= -i\hbar\left(x\frac{\partial}{\partial x}-\frac{\partial}{\partial x}x\right)\psi(x)\\ &= -i\hbar\left(x\frac{\partial \psi(x)}{\partial x}-\psi(x)-x\frac{\partial \psi(x)}{\partial x}\right)\\ &= i\hbar\psi(x)\\ \\ \therefore [\hat{x},\hat{p}] &= i\hbar \tag{1.19} \end{align} となる。
つまり、式(1.19)の交換関係は位置と運動量が測定の順序によって結果が\(\hbar\)の程度で変わることを意味し不確定性原理を定式化できていることが分かる。
6. シュレーディンガー方程式
質量\(m\)の粒子がポテンシャル\(V(x)\)の中を運動しているとき、エネルギー演算子(ハミルトニアンとよぶ)\(\hat{H}\)は\begin{align} \hat{H} &=\frac{\hat{p}^2}{2m}+V(\hat{x}) \tag{1.20} \end{align} と書ける。
シュレーディンガーの表現を用いると次のようになる。
\begin{align} \hat{H} = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x) \tag{1.21} \end{align} ハミルトニアン演算子の固有値方程式は
\begin{align} E\phi(x) &=\hat{H}\phi(x) \tag{1.22}\\ \end{align} であり、これをシュレーディンガーの表式で書き下すと次のようになる。 \begin{align} E\phi(x) &=-\frac{\hbar^2}{2m}\frac{\partial^2\phi(x)}{\partial x^2}+V(x)\phi(x) \tag{1.23} \end{align} 式(1.23)の方程式をシュレーディンガー方程式と呼ぶ。固有値\(E\)は系の全エネルギーを表す。量子力学において基本となる方程式であり、シュレーディンガー方程式を解くことで系の状態関数が求められる。
ここまでは議論を簡単にするために座標系を1次元で考えてきた。実際には位置も運動量も3次元のベクトルになる。したがって、位置演算子は、\((x, y, z)\)、運動量演算子は、\((p_x, p_y, p_z)\)の3成分を持つ。運動量演算子はシュレーディンガーの表記では次のようになる。
\begin{align} p_x = -i\hbar\frac{\partial}{\partial x}, \; p_y = -i\hbar\frac{\partial}{\partial y}, \; p_z = -i\hbar\frac{\partial}{\partial z} \tag{1.24} \end{align} これらの演算子を用いると3次元のシュレディンガー方程式は、次のようになる。ここで\(\boldsymbol{r}\)は位置ベクトルであり、\(\boldsymbol{r}=(x,y,z)\)である。
\begin{align}
E\phi(\boldsymbol{r}) &=-\frac{\hbar^2}{2m}\left(\frac{\partial^2\phi(\boldsymbol{r})}{\partial x^2}+\frac{\partial^2\phi(\boldsymbol{r})}{\partial y^2}+\frac{\partial^2\phi(\boldsymbol{r})}{\partial z^2}\right)+V(\boldsymbol{r})\phi(\boldsymbol{r}) \tag{1.25}
\end{align}
7. 角運動量
角運動量は、運動量やエネルギーと同様に保存される物理量である。そのため、量子力学においても重要な量である。ここでは量子力学における角運動量の取り扱いについて説明する。古典力学において、位置\(\boldsymbol{r}\)にいる粒子が運動量\(\boldsymbol{p}\)を持って運動しているとき、原点のまわりの角運動量\(\boldsymbol{l}\)は次のように定義される。
\begin{align} \boldsymbol{l} = \boldsymbol{r} \times \boldsymbol{p} \tag{1.26} \end{align}
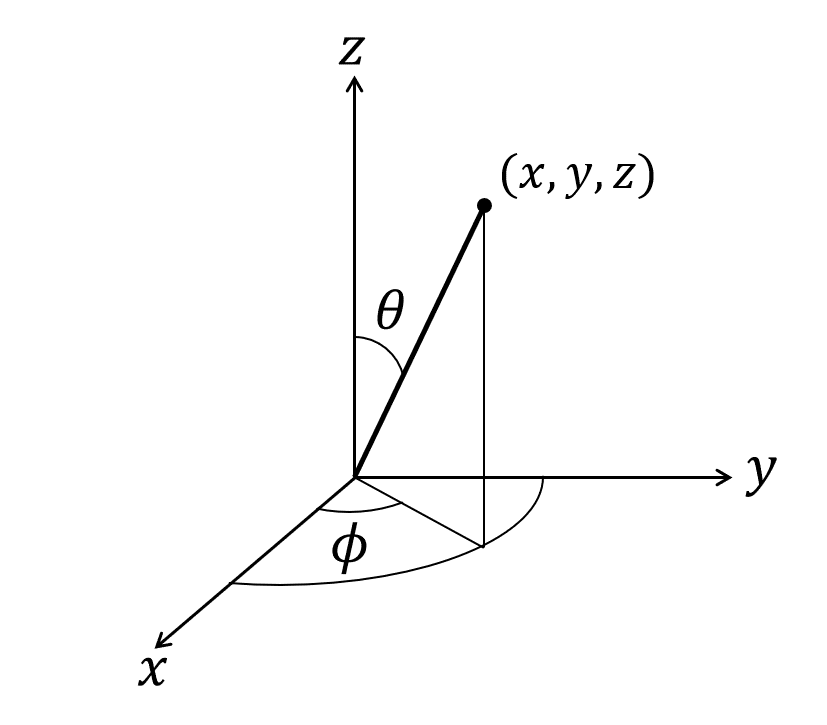
図5 球面極座標
\begin{align} \hat{l_x} &= y \hat{p_z} - z \hat{p_y} = -i\hbar\left( y\frac{\partial}{\partial z} - z\frac{\partial}{\partial y}\right) \tag{1.27}\\ \hat{l_y} &= z \hat{p_x} - x \hat{p_z} = -i\hbar\left( z\frac{\partial}{\partial x} - x\frac{\partial}{\partial z}\right) \tag{1.28}\\ \hat{l_z} &= x \hat{p_y} - y \hat{p_x} = -i\hbar\left( x\frac{\partial}{\partial y} - y\frac{\partial}{\partial x}\right) \tag{1.29} \end{align} 角運動量を取り扱いには図5の球面極座標を用いるのが便利である。球面極座標\((r, \theta, \phi)\)と直交座標\((x, y, z)\)の関係は次のようになる。
\begin{align} x &= r \sin \theta \cos \phi \\ y &= r \sin \theta \sin \phi \\ z &= r \cos \theta \end{align} 偏微分の変数変換を行うと角運動量演算子の球面極座標表示は次のようになる注9。
\begin{align} \hat{l_x} &= i\hbar\left(\sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \tag{1.30}\\ \hat{l_y} &= i\hbar\left(-\cos\phi\frac{\partial}{\partial \theta} +\frac{\sin\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \tag{1.31}\\ \hat{l_z} &= -i\hbar\frac{\partial}{\partial \phi} \tag{1.32}\\ \end{align} (\(\hat{l_z}\)の固有関数)ちなみに\(\hat{l_z}\)の固有関数は次のように簡単に求めることができる。 \begin{align} &-i\hbar\frac{\partial u(\phi)}{\partial \phi} = m\hbar u(\phi) \tag{1.33}\\ \\ &\therefore u(\phi) = e^{im\phi} \tag{1.34} \end{align} ここで\(m\hbar\)は固有値であり、便宜的に\(\hbar\)を外に出した。規格化定数も簡単のために\(1\)としている。
得られた固有関数\(e^{im\phi}\)は周期関数であり、任意の整数\(n\)に対して
\begin{align} u(\phi+2n\pi) = u(\phi) \end{align} となる。
したがって、この境界条件より\(m\)は整数でなければならない。つまり \begin{align} m = 0, \pm 1, \pm 2\; ... \tag{1.35} \end{align} である。
演算子\(\hat{l_z}\)と\(\hat{l_x}, \hat{l_y}\)の交換関係は、式から明らかなようにゼロにはならない。
\begin{align} [\hat{l_z},\hat{l_x}] \neq 0, \:\: [\hat{l_z},\hat{l_y}] \neq 0 \tag{1.36} \end{align} したがって、角運動量の\(x, y, z\)どれかの成分の固有状態が他の成分の固有状態にはならない。つまり、観測によって一成分以上の正確な値を得ることはできない。
(全角運動量)また、全角運動量の演算子も考えることができる。全角運動量は各成分の2乗和から計算できるので、全角運動量演算子\(\hat{l}^2\)は次のようになる。
\begin{align} \hat{l}^2 =\hat{l_x}^2 + \hat{l_y}^2 + \hat{l_z}^2 \tag{1.37} \end{align} 球面極座標表示の\(\hat{l_x}, \hat{l_y}, \hat{l_z}\)を用いて各成分の2乗を計算して和を取ると全角運動量演算子の球面極座標表示が得られる注10。
\begin{align} \hat{l}^2 &= -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) \tag{1.38} \end{align} 角運動量演算子の球面極座標表示を以下にまとめる。
\begin{align}
\hat{l_x} &= i\hbar\left(\sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \tag{1.39}\\
\hat{l_y} &= i\hbar\left(-\cos\phi\frac{\partial}{\partial \theta} +\frac{\sin\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \tag{1.40}\\
\hat{l_z} &= -i\hbar\frac{\partial}{\partial \phi} \tag{1.41}\\
\hat{l}^2 &= -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) \tag{1.42}
\end{align}
(\(\hat{l}^2\)の固有関数)式(1.41)と(1.42)から容易に\(\hat{l_z}\)と\(\hat{l}^2\)の交換関係がゼロであることが分かる注11。\begin{align} [\hat{l_z},\hat{l}^2] =0 \tag{1.43} \end{align} したがって、全角運動量と角運動量の\(z\)成分を同時に正確に知ることができる。つまり、2つの演算子\(\hat{l}^2\)と\(\hat{l_z}\)の同時固有関数\(Y_{\beta m}(\theta,\phi)\)が存在し、次の固有値方程式を満たす。
\begin{align} \hat{l_z}Y_{\beta m}(\theta,\phi) &= m \hbar Y_{\beta m}(\theta,\phi) \tag{1.44}\\ \hat{l}^2 Y_{\beta m}(\theta,\phi) &= \beta \hbar^2 Y_{\beta m}(\theta,\phi) \tag{1.45} \end{align} \(\hat{l}^2\)の固有値は、便宜的に\(\hbar^2\)を外に出した。
この\(\hat{l_z}\)の固有関数は式(1.34)で既に求めたように\(e^{im\phi}\)である。したがって、\(Y_{\beta m}(\theta,\phi)\)は次のように書ける。
\begin{align} Y_{\beta m}(\theta,\phi)=P_{\beta m}(\theta)e^{im\phi} \tag{1.46} \end{align} 演算子\(\hat{l}^2\)を作用させると
\begin{align} \hat{l}^2 P_{\beta m}(\theta)e^{im\phi} &= -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right)P_{\beta m}(\theta)e^{im\phi}\\ &= -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{m^2}{\sin^2\theta}\right)P_{\beta m}(\theta)e^{im\phi}\\ \end{align} となり、以下の\(P_{\beta m}(\theta)\)に関する固有値方程式が得られる。 \begin{align} \left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{m^2}{\sin^2\theta}\right)P_{\beta m}(\theta) = -\beta P_{\beta m}(\theta) \tag{1.47} \end{align} さらに
\begin{align} w = \cos\theta \tag{1.48} \end{align} とすると
\begin{align} \frac{1}{\sin\theta}\frac{d}{d\theta} = -\frac{d}{dw} \tag{1.49} \end{align} なので、式(1.47)は\(w\)を用いて次の方程式に書きかえられる注12。
\begin{align} \frac{d}{dw}(1-w^2)\frac{dP_{\beta m}}{dw} + \left(\beta - \frac{m^2}{1-w^2}\right)P_{\beta m} = 0 \tag{1.50} \end{align} この方程式の解は\(-1 < w < 1\)(すなわち\(-1 < \cos\theta < 1\)または\(0 < \theta < 2\pi \))で有限の値を持つという境界条件を与えたとき、ルジャンドルの陪多項式とよばれる特殊関数となることが知られている。式(1.50)を解いてルジャンドル陪多項式をもとめる解法については多くの参考書で解説されているのでそちらを参照されたい文献7。重要なことは先人たちが式(1.50)の解を特殊関数という形でまとめてくれている点である。おかげで我々はその恩恵に預かることができる。特殊関数と聞くと難しいと感じる人もいるかもしれないが、ユーザーという観点からすれば先人がまとめてくれた関数を使うというスタンスで十分である。
境界条件からルジャンドル陪多項式\(P_{\beta m}(w)\)の\(\beta\)が許される値は、\(l\)を整数(\(l=0, 1, 2 ...\))とすると次のようになる。
\begin{align} \beta = l(l+1) \tag{1.51} \end{align} また、\(\beta = l(l+1)\)のとき、許される\(m\)は以下の\((2l+1)\)個の値である
\begin{align} m=0, \pm 1, \pm 2, \cdots, \pm l \tag{1.52} \end{align} ルジャンドル陪多項式の次数を指定するには\(\beta\)よりも\(l\)の方が便利なので以後、\(P_{l m}(w)\)と書く。ルジャンドル陪多項式の具体的な形は参考文献で与えられている文献8。\(l=2\)までのものを以下に上げておく。
\begin{align}
&P_{0 0}(w) = 1 \tag{1.53}\\
&P_{1 0}(w) = w \tag{1.54}\\
&P_{1 1}(w) = -(1-w^2)^{\frac{1}{2}} \tag{1.55}\\
&P_{2 0}(w)= \frac{1}{2}(3 w^2 -1) \tag{1.56}\\
&P_{2 1}(w) = -3w (1-w^2)^{\frac{1}{2}} \tag{1.57}\\
&P_{2 2}(w) = 3(1-w^2) \tag{1.58}
\end{align}
(球面調和関数)以上の結果から、ルジャンドル陪多項式を用いて方程式(1.44)(1.45)の固有関数を書くと次のようになる。\begin{align} Y_{l m}(\theta,\phi)= i^{m+|m|}\left(\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}\right)P_{l m}(\cos\theta)e^{im\phi} \tag{1.59} \end{align}

図6 角運動量のベクトル図
\begin{align} \int^{2\pi}_0\int^{\pi}_0 Y_{l m}^*(\theta,\phi) Y_{l m}(\theta,\phi) d\theta d\phi = 1 \tag{1.60} \end{align} \(\hat{l}^2\)と\(\hat{l_z}\)の固有値は、それぞれ次のようになる。
\begin{align} \beta\hbar^2 = l(l+1)\hbar^2,\: l=0,1,2,\cdots \tag{1.61}\\ l_z = m\hbar,\: m=0, \pm 1, \pm 2, \cdots, \pm l \tag{1.62} \end{align} \(Y_{l m}(\theta,\phi)\)は球面調和関数とよばれ、大きさ\(l\hbar\) 注13、\(z\)成分が\(m\hbar\)の軌道角運動量を持つ粒子の波動関数である注14。このことは角運動量の大きさが\(\hbar\)を単位として飛び飛びの値を取ることを意味する。また、\(l_z\)も\(\hbar\)を単位として飛び飛びの値を取る。エネルギーや運動量の観測値は離散的な値をとるか連続的な値をとるかは系の状態によるが、軌道角運動量に関してはどんな場合でも\(\hbar\)を単位とする離散的な値しか許されない注15。古典的には図6のようなベクトル図で表される(図は\(l=4\)の場合)。\(\theta=0\)のときに\(l_z\)は最大となり、\(\theta=\pi\)のときに最小となる。また、\(0<\theta<\pi\)の間の途中の値も取ることができるが、\(\hbar\)を単位として離散的になる。
以下に球面調和関数の\(l=2\)までの関数を参考に示す。
\begin{align}
&Y_{0 0}(\theta,\phi) = \frac{1}{\sqrt{4\pi}} \tag{1.63}\\
&Y_{1 0}(\theta,\phi) = \sqrt{\frac{3}{4\pi}} \cos \theta \tag{1.64}\\
&Y_{1 \pm 1}(\theta,\phi) = \mp \sqrt{\frac{3}{8\pi}} \sin \theta e^{\pm i \phi}\tag{1.65}\\
&Y_{2 0}(\theta,\phi)= \sqrt{\frac{5}{16\pi}} (3\cos^2 \theta -1) \tag{1.66}\\
&Y_{2 \pm 1}(\theta,\phi) = \mp \sqrt{\frac{15}{8\pi}} \sin \theta \cos \theta e^{\pm i \phi} \tag{1.67}\\
&Y_{2 \pm 2}(\theta,\phi) = \sqrt{\frac{15}{32\pi}} \sin^2 \theta e^{\pm 2 i \phi} \tag{1.68}
\end{align}
8. 束縛状態
粒子が引力ポテンシャルに束縛され有限の空間領域に閉じ込められている状態を束縛状態とよぶ。例えば、水素原子の中の電子が挙げられる。電子は、陽子の作るクーロンポテンシャル中に束縛されている。よく知られているように水素原子のエネルギー準位は飛び飛びの離散的な値をとる。これは束縛状態の一般的な性質で水素原子に限らず束縛状態が取りうるエネルギーは離散的な値しか許されない。このエネルギー準位が離散的になるという性質は粒子の波動性と密接に結びついている。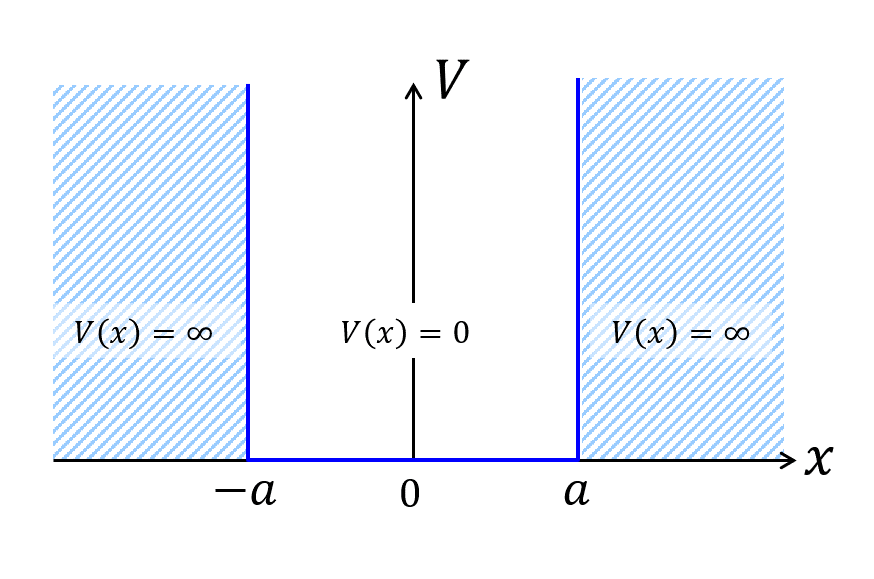
図7 1次元の無限に深い井戸型ポテンシャル
\begin{align} V(x) = \left\{ \begin{array}{ll} 0 & (|x| \leq a) \tag{1.69}\\ \infty & (|x| \gt a) \end{array} \right. \end{align} 粒子は\(-a < x < a\)の領域では全く力を受けないが、\(x \pm a\)でポテンシャルの壁により弾性的に跳ね返され、どんなに大きな運動エネルギーを持っていてもポテンシャルの外の領域に出ることはできない。
このとき、シュレーディンガー方程式は次のようになる。
\begin{align} E\psi(x) &=-\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2}+V(x)\psi(x) \tag{1.70} \end{align} 粒子はポテンシャルの外(\(|x| \gt a\))には存在しないので、境界条件としてを以下を満たさなくてはならない。
\begin{align} \psi(a) = 0, \quad \psi(-a) = 0 \tag{1.71} \end{align} 式(1.69)から\(|x| \leq a\)で\(V(x)=0\)なので式(1.70)の方程式は次のようになる。 \begin{align} &E\psi(x) =-\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2} \tag{1.72}\\ &\therefore \frac{\partial^2\psi(x)}{\partial x^2}+k^2\psi(x)=0 \tag{1.73} \end{align} ここで\(k\)は
\begin{align} k = \frac{\sqrt{2mE}}{\hbar} \tag{1.74} \end{align}

図8 無限に深い井戸型ポテンシャルの固有状態
\begin{align} &\psi(x) = A\sin (k_{2n}x) \tag{1.75}\\ &k_{2n}=2n\frac{\pi}{2a} \qquad (n=1,2,\cdots) \tag{1.76} \end{align} または \begin{align} &\psi(x) = B\cos (k_{2n+1}x) \tag{1.77}\\ &k_{2n+1}=(2n+1)\frac{\pi}{2a} \qquad (n=0,1,2,\cdots) \tag{1.78} \end{align} である。
式(1.75)と(1.77)を一緒に書くと
\begin{align} k_{n}=\left(\frac{\pi}{2a}\right)n \qquad (n=1,2,\cdots) \tag{1.79} \end{align} となり、エネルギーは
\begin{align} E_n=\frac{\hbar^2}{2m}\left(\frac{\pi}{2a}\right)^2n^2 \tag{1.80} \end{align} となる。すなわち取りうるエネルギーが離散的になることがわかる。
図8に\(n=4\)までの固有状態を示す。\(n\)が一つ大きくなるごとに波の節が一つ増えていく。波動関数の形は古典力学で扱う両端を固定された弦の振動と全く同じであることが分かる。井戸型ポテンシャル中の粒子のエネルギーが離散的になる点も、弦の振動において許される振動数が飛び飛びの値になることと同じである。
束縛状態のエネルギーの量子化は、古典的な弦の振動との対応でも分かるように、波動が空間的に閉じ込められていることが原因である。ポテンシャルの形がどんなものであれ、粒子がある空間内に束縛されれば固有状態のエネルギー値は離散化する注16。
(中心力ポテンシャルのシュレーディンガー方程式)ここでは、ポテンシャルが原点からの距離\(r\)のみに依存する場合、すなわち中心力ポテンシャル中の粒子の運動を扱う。ポテンシャルは\(r\)にしか依存しないので
\begin{align} V(\boldsymbol{r}) \rightarrow V(r) \tag{1.81} \end{align} となり、3次元のシュレーディンガー方程式は次のように書ける。
\begin{align} E\psi(\boldsymbol{r}) &=-\frac{\hbar^2}{2m}\left(\frac{\partial^2\psi(\boldsymbol{r})}{\partial x^2}+\frac{\partial^2\psi(\boldsymbol{r})}{\partial y^2}+\frac{\partial^2\psi(\boldsymbol{r})}{\partial z^2}\right)+V(r)\psi(\boldsymbol{r}) \tag{1.82} \end{align} 球面極座標表示で表すと次のように書ける注17。
\begin{align} E\psi(r, \theta, \phi) & = \left\{-\frac{\hbar^2}{2m}\left(\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r}) +\frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) + V(r)\right\}\psi(r, \theta, \phi) \tag{1.83} \end{align} この方程式の\(\theta, \phi\)依存性は、全角運動量演算子\(\hat{l}^2\)と全く同じである。したがって、次のように書くことができる注18。
\begin{align} E\psi(r, \theta, \phi) & = \left(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{\hat{l}^2}{2 m r^2}+ V(r)\right)\psi(r, \theta, \phi) \tag{1.84} \end{align} ハミルトニアンの第1項、第3項は、\(\theta, \phi\)に依存しないので、ハミルトニアンは\(\hat{H}\)は演算子\(\hat{l}^2, \hat{l_z}\)と交換可能である。すなわち \begin{align} [\hat{H},\hat{l}^2] =0, \: [\hat{H},\hat{l_z}] =0 \tag{1.85} \end{align} である。したがって、中心力ポテンシャル中を運動する粒子に対しては、エネルギー、全角運動量、角運動量の\(z\)成分を同時に決定することができる。このとき、方程式は変数分離することができて固有関数は次のように\(r\)のみに依存する関数\(R_n(r)\)と\(\hat{l}^2, \hat{l_z}\)の固有関数\(Y_{l m}(\theta,\phi)\)の積で書くことができる。
\begin{align} \psi(r, \theta, \phi) = R_n(r) Y_{l m}(\theta,\phi) \tag{1.86} \end{align} ここで\(n\)は動径方向の波動関数の量子数である。波動関数は、\(n, l, m\)の3つの量子数によって指定される。式(1.86)を式(1.84)に代入すると\(\hat{l}^2\)は固有値\(l(l+1)\hbar^2\)で置き換えられるので
\begin{align} E_{nl} R_n(r) Y_{l m}(\theta,\phi) & = \left(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{l(l+1)\hbar^2}{2 m r^2}+ V(r)\right)R_n(r) Y_{l m}(\theta,\phi) \tag{1.87} \end{align} となる。ハミルトニアンには\(\hat{l_z}\)は陽に現れていないので固有値は磁気量子数\(m\)には依存しない。そのため固有値は\(n,l\)のみに依存するので\(E_{nl}\)と表記した。
式(1.87)の両辺の\(Y_{l m}(\theta,\phi)\)を除すると以下の\(R_n(r)\)についての方程式が得られる。
\begin{align} E_{nl} R_n(r) & = \left(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{l(l+1)\hbar^2}{2 m r^2}+ V(r)\right)R_n(r) \tag{1.88} \end{align} 中心力ポテンシャルの場合、\(\theta,\phi\)成分の波動関数は\(Y_{l m}(\theta,\phi)\)で既に与えられているので、上記の動径成分に対する固有値方程式を解けば波動関数\(\psi(r, \theta, \phi)\)が決まる。ちなみに右辺括弧内の第2項は遠心力ポテンシャルとも呼ばれ、見かけ上の斥力ポテンシャルとして働く。\(l=1\)以上で働き、\(l\)が大きくなるほど波動関数を動径方向に、より外側に分布させる効果を及ぼす。
9. 状態の重ね合わせ、観測可能な演算子、確率分布
ここまでは主にシュレーディンガー方程式の固有関数を求めることについて述べてきた。ここでは、量子力学のより一般的な理論的枠組について述べる。(重ね合わせの原理)まず、波動関数には重ね合わせの原理が成り立つ。つまり、2つ以上の波動関数を足し合わせて別の状態を作ることができる。例えば、\(\psi_1, \psi_2\)という2つの波動関数があったとして、それらを足し合わせて、\(\psi_3\)という状態を作ることができる。
\begin{align} \psi_3 = \psi_1 + \psi_2 \tag{1.89} \end{align} (重なりの積分)2つの波動関数\(\psi_1, \psi_2\)が似ている度合いは以下の重なりの積分により定量的に評価される。
\begin{align} \int\psi_1^*(x)\psi_2(x)dx \tag{1.90} \end{align} ただし、簡単のために1次元としている注19。2つの波動関数の重なる面積が大きいほど式(1.90)の積分値は大きくなる。特別な場合として一つの波動関数自身で重なりの積分を行うと
\begin{align} \int\psi^*(x)\psi(x)dx = \int|\psi(x)|^2dx \tag{1.91} \end{align} となり、結果は実数となる。
(規格化)波動関数は任意の定数をかけても物理的な帰結は変わらない。そこで、この任意性をなくすために式(1.91)の積分が\(1\)となるように以下の制限を加えることとする。これを規格化と呼ぶ。
\begin{align} \int\psi^*(x)\psi(x)dx = \int|\psi(x)|^2dx = 1 \tag{1.92} \end{align} これ以降の議論では特にことわりがなければ波動関数は規格化されているものとする。
(測定値の平均値)式(1.13)で計算される観測\(\hat{A}\)を行ったときの平均値は、規格化された波動関数を用いると次のように簡単な式になる。
\begin{align} \langle a\rangle = \int\psi^*(x)\hat{A}\psi(x)dx \tag{1.93} \end{align} (観測可能な演算子)測定で得られる物理量は実数でなくてはならない。したがって、式(1.93)で計算される量は任意の波動関数\(\psi\)に対して次の条件を満たす注20。
\begin{align} \int\psi^*(x)\hat{A}\psi(x)dx = \left[\int\psi^*(x)\hat{A}\psi(x)dx \right]^* \tag{1.94} \end{align} これは観測量が実数になるための必要条件であるが、演算子に対しさらに強い次の制限を課すことにする。
物理的に観測可能な量を表す演算子は任意の波動関数\(\phi,\psi\)に対し、以下の式を満たさなければならない注21。
\begin{align} \int\phi^*(x)\hat{A}\psi(x)dx = \left[\int\psi^*(x)\hat{A}\phi(x)dx \right]^* \tag{1.95} \end{align} このような演算子を観測可能な演算子と呼ぶ注22。
さらに式(1.95)から、観測可能な演算子の固有関数は実数であることが導き出される。観測可能な演算子\(\hat{A}\)の固有関数を\(u(x)\)、固有値を\(a\)とすると\begin{align} \int\phi^*(x)\hat{A}\psi(x)dx = \left[\int\psi^*(x)\hat{A}\phi(x)dx \right]^* \tag{1.95} \end{align} このような演算子を観測可能な演算子と呼ぶ注22。
\begin{align} \hat{A} u(x) = a u(x) \tag{1.96} \end{align} である。左から\(u^*(x)\)を乗じて積分すると
\begin{align} \int u^*(x) \hat{A} u(x) dx &= \int u^*(x) a u(x) dx \tag{1.97}\\ &= a\int |u(x)|^2 dx \\ \therefore \int u^*(x) \hat{A} u(x) dx &= a \tag{1.98} \end{align} となる。式(1.98)の左辺は式(1.95)から実数である。したがって、固有値\(a\)も実数となる。
(固有関数の直交性)式(1.90)で定義される2つの波動関数の重なりの積分が\(0\)になるとき、2つの波動関数は直交するという。 \begin{align} \int\psi_1^*(x)\psi_2(x)dx = 0 \tag{1.99} \end{align} 異なる固有値に属する2つの固有関数は直交する。すなわち、観測可能な演算子\(\hat{A}\)に対する2つの異なる固有関数\(u_1(x), u_2(x)\)があるとき、次のように重なりの積分は\(0\)になる(証明は注23を参照のこと)
\begin{align} \int u_2^*(x) u_1(x) dx = 0 \tag{1.100} \end{align} (完全性)観測可能な演算子に対し、式(1.95)に加えさらに次の仮定を加える。
観測可能な演算子は、その固有関数が完全系を作らなければならない。
\begin{align} \psi(x) = c_0 u_0(x) + c_1 u_1(x) + c_2 u_2(x) + \cdots = \sum_i c_i u_i(x) \tag{1.101} \end{align} ここで\(c_i\)は展開係数である。逆に\(c_i\)が与えられれば、波動関数\(\psi(x)\)は記述できる。
(確率分布)以上、ここまで述べたことを用いて、一般の状態に対して観測を行ったときの測定値の確率分布について、もう一度考察しよう。
一般の状態に対して観測\(\hat{A}\)を行ったときの測定値の平均\(\langle a\rangle\)は式(1.93)で与えられることを述べた。すなわち、
\begin{align} \langle a\rangle = \int\psi^*(x)\hat{A}\psi(x)dx \tag{1.102} \end{align} である。
まず、一番簡単な演算子として位置演算子\(\hat{A}=x\)について見てみよう。代入すると
\begin{align} \langle x\rangle &= \int\psi^*(x)x\psi(x)dx \\ &= \int x|\psi(x)|^2 dx \tag{1.103} \end{align} となる。この式で\(|\psi(x)|^2\)は、\(x\)の平均値を計算する際の重みの関数となっている。このことから、よく知られている以下の波動関数の直接的な解釈が導かれる。
波動関数は、その絶対値の2乗が空間における粒子の存在の確率密度を表す。
\begin{align} \psi(x) = c_0 u_0(x) + c_1 u_1(x) + c_2 u_2(x) + \cdots \tag{1.104} \end{align} これを式(1.102)に代入すると
\begin{align} \langle a\rangle &= \int\psi^*(x)\hat{A}\psi(x)dx \\ &= \int (c_0^* u_0^*(x) + c_1^* u_1^*(x) + c_2^* u_2^*(x) + \cdots )\hat{A}(c_0 u_0(x) + c_1 u_1(x) + c_2 u_2(x) + \cdots )dx \\ &= \int (c_0^* u_0^*(x) + c_1^* u_1^*(x) + c_2^* u_2^*(x) + \cdots )(a_0 c_0 u_0(x) + a_1 c_1 u_1(x) + a_2 c_2 u_2(x) + \cdots )dx \tag{1.105} \end{align} となる。ここで固有関数は直交性から、同一の固有関数の重なりの積分は\(1\)となり、それ以外は全て\(0\)となる。つまり、
\begin{align} \int u_i^*(x) u_i(x) dx &= 1 \tag{1.106} \\ \int u_i^*(x) u_j(x) dx &= 0 \; (i \neq j) \tag{1.107} \end{align} である。したがって、式(1.105)は
\begin{align} \langle a\rangle = \int\psi^*(x)\hat{A}\psi(x)dx = a_0 |c_0|^2 + a_1 |c_1|^2 + a_2 |c_2|^2 + \cdots = \sum_i a_i |c_i|^2 \tag{1.108} \end{align} となる。式(1.108)から、\(|c_i|^2\)が測定値の平均を計算する際の重みとなっていることがわかる。したがって、以下の結論が導かれる。
状態\(\psi\)に対し観測\(\hat{A}\)を行ったとき、測定値が固有値\(a_i\)となる確率は、\(\psi\)を\(\hat{A}\)の固有関数の線形結合で表したときの展開係数\(c_i\)の絶対値の2乗により与えられる。
10. まとめ
以上、ざっとではあるが、核データの入門的な解説を理解する上で最低限必要な量子力学の基礎について述べた。次章以降では核データの具体的な項目について解説していく。また、本章は、初学者のために分かりやすさを優先し理論の厳密性にはこだわらなかった。ブラケットを用いたディラック記法なども解説しなかった。さらに詳しく勉強したい読者にはぜひ、より専門的な量子力学の教科書を読むことをすすめる。注釈
- 1895年のレントゲンによるX線の発見を皮切りに、ベクレルによる放射能の発見(1896)、トムソンによる電子の発見(1897)、ラザフォードによるアルファ線とベータ線の発見(1898)と発見のゴールドラッシュが(これ以降も)続いた。
- 光の粒子性が現れた最初の徴候は、黒体輻射の問題である。プランクがこの問題を扱い、プランク定数を導入した量子仮説により説明できることを示した。ただし、この現象は入門として扱うには少し難しいのでここでは取り上げなかった。
- ラボアジェやドルトンなどの研究から原子論が提唱され化学反応をよく説明できることは知られていた。また、19世紀にはマクスウェルやボルツマンが原子論を物理学に適用した気体分子運動論などの理論研究が行われた。しかし、19世紀後半になっても原子論は科学者の主流派・多数派に受け入れられていなかった。その理由は直接観測できないものは受け入れられないという姿勢に尽きる。原子論が疑いなく認められるようになったのは実に20世紀初頭になって数々の原子や原子核の現象が見つかってからである。
- 実際にこの実験をやるとなると非常に大変である。なぜなら、電子の波動としての波長はとても短く、その干渉効果を見るには2つのスリット間隔を原子サイズ程度にしなくてはならないからである。
- 古典力学で波動や振動を扱う際に振幅を複素数で表現して問題を解く場合があるが、あくまで数学上のテクニックである。量子力学の波動関数は複素数で記述しないと理論が成り立たない。
- これを集団とかアンサンブルと呼ぶことがある。
- \(\psi^*(x)\)は\(\psi(x)\)の複素共役である。\(c=a+ib\)という複素数(\(a,b\)は実数)に対し、複素共役は\(c^*=a-ib\)である。複素共役との積は、
\begin{align} c^* c = (a-ib)(a+ib)=a^2+b^2 \end{align} となり、複素数の絶対値の2乗となる。式(1.13)の積分は全空間を積分区間とする。 - 実際には位置は3次元の座標で記述されるので位置演算子は\(x, y, z\)の3成分が必要である。運動量も同様に\(p_x, p_y, p_z\)の3成分が必要である。ここでは議論を簡単にするために1次元で考えている。
- 角運動量演算子の球面極座標表示は、以下の偏微分の変換式から求めることができる。
\begin{align} \frac{\partial}{\partial \theta} &= \frac{\partial x}{\partial \theta}\frac{\partial}{\partial x} + \frac{\partial y}{\partial \theta}\frac{\partial}{\partial y} + \frac{\partial z}{\partial \theta}\frac{\partial}{\partial z} = r\cos \theta \cos \phi\frac{\partial}{\partial x} + r\cos \theta \sin \phi\frac{\partial}{\partial y} - r\sin \theta \frac{\partial}{\partial z}\\ \frac{\partial}{\partial \phi} &= \frac{\partial x}{\partial \phi}\frac{\partial}{\partial x} + \frac{\partial y}{\partial \phi}\frac{\partial}{\partial y} + \frac{\partial z}{\partial \phi}\frac{\partial}{\partial z} = -r \sin \theta \sin \phi \frac{\partial}{\partial x} + r\sin \theta \cos \phi \frac{\partial}{\partial y} \tag{1.109} \end{align} まず、式(1.109)は、
\begin{align} \frac{\partial}{\partial \phi} &= -r \sin \theta \sin \phi \frac{\partial}{\partial x} + r\sin \theta \cos \phi \frac{\partial}{\partial y}\\ &= -y\frac{\partial}{\partial x}+x\frac{\partial}{\partial y} \end{align} となるので、\(\hat{l_z}\)は簡単に書き換えることができて
\begin{align} \hat{l_z} &= -i\hbar\left( x\frac{\partial}{\partial y} - y\frac{\partial}{\partial x}\right) = -i\hbar\frac{\partial}{\partial \phi} \end{align} となる。
\(\hat{l_x}\)については、
\begin{align} \sin\phi\frac{\partial}{\partial \theta} &= r\cos \theta \sin\phi\cos \phi\frac{\partial}{\partial x} + r\cos \theta \sin^2 \phi\frac{\partial}{\partial y} - r\sin \theta\sin\phi \frac{\partial}{\partial z}\\ \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi} &= -r \cos\theta \sin\phi\cos\phi \frac{\partial}{\partial x} + r\cos \theta \cos^2 \phi \frac{\partial}{\partial y} \end{align} の2項の和をとると
\begin{align} \sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}&= r\cos \theta \frac{\partial}{\partial y} - r\sin \theta\sin\phi \frac{\partial}{\partial z}\\ &= z\frac{\partial}{\partial y} - y\frac{\partial}{\partial z} \end{align} となるので、\(\hat{l_x}\)は、次のように書き換えられる。
\begin{align} \hat{l_x} &= -i\hbar\left( y\frac{\partial}{\partial z} - z\frac{\partial}{\partial y}\right)\\ &= i\hbar\left(\sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \end{align} \(\hat{l_y}\)も同様に
\begin{align} \cos\phi\frac{\partial}{\partial \theta} &= r\cos \theta \cos^2 \phi\frac{\partial}{\partial x} + r\cos \theta \sin \phi\cos\phi\frac{\partial}{\partial y} - r\sin \theta\cos\phi\frac{\partial}{\partial z}\\ \frac{\sin\phi}{\tan\theta}\frac{\partial}{\partial \phi} &= -r \cos\theta \sin^2\phi \frac{\partial}{\partial x} + r\cos \theta \sin\phi\cos \phi \frac{\partial}{\partial y} \end{align} の2項の差をとると
\begin{align} \cos\phi\frac{\partial}{\partial \theta} -\frac{\sin\phi}{\tan\theta}\frac{\partial}{\partial \phi} &= r\cos \theta \frac{\partial}{\partial x} - r\sin \theta\cos\phi \frac{\partial}{\partial z}\\ &= z\frac{\partial}{\partial x} - x\frac{\partial}{\partial z} \end{align} となるので、\(\hat{l_y}\)は、
\begin{align} \hat{l_y} &= -i\hbar\left( z\frac{\partial}{\partial x} - x\frac{\partial}{\partial z}\right)\\ &= i\hbar\left(-\cos\phi\frac{\partial}{\partial \theta} +\frac{\sin\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right) \end{align} となる。
- 以下、導出を示す。
\begin{align}
\hat{l_x}^2 &= -\hbar^2\left(\sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right)\left(\sin\phi\frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta}\frac{\partial}{\partial \phi}\right)\\
&=-\hbar^2\left(\sin^2\phi\frac{\partial^2}{\partial \theta^2} - \frac{\sin\phi\cos\phi}{\sin^2\theta}\frac{\partial}{\partial \phi} + 2\frac{\sin\phi\cos\phi}{\tan\theta}\frac{\partial^2}{\partial\theta\partial\phi} + \frac{\cos^2\phi}{\tan\theta}\frac{\partial}{\partial\theta} - \frac{\sin\phi\cos\phi}{\tan^2\theta}\frac{\partial}{\partial\phi} + \frac{\cos^2\phi}{\tan^2\theta}\frac{\partial^2}{\partial\phi^2} \right)\\
\hat{l_y}^2 &= -\hbar^2\left(\cos^2\phi\frac{\partial^2}{\partial \theta^2} + \frac{\sin\phi\cos\phi}{\sin^2\theta}\frac{\partial}{\partial \phi} - 2\frac{\sin\phi\cos\phi}{\tan\theta}\frac{\partial^2}{\partial\theta\partial\phi} + \frac{\sin^2\phi}{\tan\theta}\frac{\partial}{\partial\theta} + \frac{\sin\phi\cos\phi}{\tan^2\theta}\frac{\partial}{\partial\phi} + \frac{\sin^2\phi}{\tan^2\theta}\frac{\partial^2}{\partial\phi^2} \right)\\
\hat{l_z}^2 &= -\hbar^2\frac{\partial^2}{\partial \phi^2}
\end{align}
となり、この和を取ると全角運動量演算子の球面極座標表示が得られる。
\begin{align}
\hat{l}^2 &= \hat{l_x}^2 + \hat{l_y}^2 + \hat{l_z}^2\\
&= -\hbar^2\left(\frac{\partial^2}{\partial \theta^2} + \frac{1}{\tan\theta}\frac{\partial}{\partial\theta} + \frac{1}{\tan^2\theta}\frac{\partial^2}{\partial\phi^2} + \frac{\partial^2}{\partial \phi^2}\right) \\
&= -\hbar^2\left(\frac{\partial^2}{\partial \theta^2} + \frac{1}{\tan\theta}\frac{\partial}{\partial\theta} + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) \\
&= -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right)
\end{align}
ここで以下の関係を用いた。
\begin{align} \frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) = \frac{\partial^2}{\partial \theta^2} + \frac{1}{\tan\theta}\frac{\partial}{\partial\theta} \end{align} - \(\frac{\partial}{\partial \phi}\)以外に\(\phi\)を含んだ因子がない。
- 以下のように求まる。
\begin{align}
&\left(\frac{d}{dw}(\sin^2\theta\frac{d}{dw}) + \frac{m^2}{\sin^2\theta}\right)P_{\beta m}(w) = -\beta P_{\beta m}(w)\\
&\left(\frac{d}{dw}((1-\cos^2\theta)\frac{d}{dw}) + \frac{m^2}{1-\cos^2\theta}\right)P_{\beta m}(w) = -\beta P_{\beta m}(w)\\
&\frac{d}{dw}(1-w^2)\frac{dP_{\beta m}(w)}{dw} + \frac{m^2}{1-w^2}P_{\beta m}(w) = -\beta P_{\beta m}(w)\\
&\therefore \frac{d}{dw}(1-w^2)\frac{dP_{\beta m}}{dw} + \left(\beta - \frac{m^2}{1-w^2}\right)P_{\beta m} = 0
\end{align}
- \(\hat{l}^2\)の固有値が\(l(l+1)\hbar^2\)なので角運動量の大きさは正確には\(\sqrt{l(l+1)}\hbar\)だが、慣例で\(l\hbar\)を大きさと言うことが多い。
- 正確には波動関数の\(\theta, \phi\)依存性である。当たり前だが波動関数の\(r\)依存性は含まれていない。別に与える必要がある。
- ただし、スピン角運動量の場合には\(\frac{1}{2} \hbar\)のような半整数が許される。
- もちろん、許されるエネルギーの値はポテンシャルの形に依存する。
- シュレーディンガー方程式の球面極座標表示は次のように求めることができる。
- この式は古典力学的にも理解しやすいものである。
- 一般には3次元なので重なりの積分は次のようになる。
\begin{align} \int\int\int\psi_1^*(x,y,z)\psi_2(x,y,z)dxdydz \end{align} - 実数なので複素共役を取っても何も変わらない。つまり、式で書くと次のようになる。
\begin{align}
R = R^*
\end{align}
- これを演算子のエルミート性という。
- オブザーバブルとも呼ぶ。
- 観測可能な演算子\(\hat{A}\)に対する2つの異なる固有関数\(u_1(x), u_2(x)\)があり、それぞれの固有値を\(a_1, a_2\)とする。すなわち
\begin{align} \hat{A} u_1(x) &= a_1 u_1(x)\\ \hat{A} u_2(x) &= a_2 u_2(x) \end{align} である。左から、それぞれ\(u_2^*(x), u_1^*(x)\)を乗じて積分すると
\begin{align} \int u_2^*(x)\hat{A} u_1(x) dx &= a_1 \int u_2^*(x) u_1(x) dx \tag{1.110}\\ \int u_1^*(x)\hat{A} u_2(x) dx &= a_2 \int u_1^*(x) u_2(x) dx \tag{1.111} \end{align} となる。式(1.111)の複素共役を取ると
\begin{align} \left[\int u_1^*(x)\hat{A} u_2(x) dx\right]^* &= \left[a_2 \int u_1^*(x) u_2(x) dx \right]^* \tag{1.112} \end{align} である。左辺は、式(1.95)より
\begin{align} \left[\int u_1^*(x)\hat{A} u_2(x) dx\right]^* &= \int u_2^*(x)\hat{A} u_1(x) dx \tag{1.113} \end{align} となる。また、式(1.112)の右辺は、\(a_2\)が観測可能な演算子の固有値なので実数である。したがって、
\begin{align} \left[a_2 \int u_1^*(x) u_2(x) dx \right]^* &= a_2 \left[\int u_1^*(x) u_2(x) dx \right]^*\\ &= a_2 \int u_1(x) u_2^*(x) dx \\ &= a_2 \int u_2^*(x) u_1(x) dx \tag{1.114} \end{align} となる。式(1.113)と式(1.114)から
\begin{align} \int u_2^*(x)\hat{A} u_1(x) dx = a_2 \int u_2^*(x) u_1(x) dx \tag{1.115} \end{align} となる。式(1.110)から式(1.115)を引くと\begin{align} 0 = (a_1 - a_2) \int u_2^*(x) u_1(x) dx \end{align} となる。2つの固有値\(a_1, a_2\)は等しくないので、\(a_1 - a_2 \neq 0\)である。したがって、右辺の重なりの積分が\(0\)でなければならない。すなわち
\begin{align} \int u_2^*(x) u_1(x) dx = 0 \end{align} であり、2つの異なる固有値に属する固有関数\(u_1(x), u_2(x)\)は直交することが示された。
参考文献
- H. Hertz, Annalen der Physik. 267, 983 (1887).
- A. Einstein, Annalen der Physik, 17, 132 (1905).
- A. H. Compton, Physical Review 21, 483 (1923).
- L. de Broglie, Annales de Physique, 3, 22 (1925).
- C. Davisson and L. H. Germer, Nature 119, 558 (1927).
- R. P. Feynman, 砂川重信 訳「ファインマン物理学」第5巻、岩波書店
原文の英語版は以下のサイトでも公開されている。
Feynman Lectures on Physics. https://www.feynmanlectures.caltech.edu/ - ジョージ・アルフケン「特殊関数」講談社
- 森口繁一, 一松信 他「数学公式集 III 特殊函数」岩波書店