第2章 原子核反応の概要 初級編
東京工業大学 片渕竜也
目次
1. はじめに
本章では、原子核反応の基礎的な知識として、クーロン障壁、原子核反応の表記法、反応のQ値、断面積、運動学について学ぶ。運動学については、古典的な力学の知識で十分理解できることから、実験室系と重心系を用いた計算などある程度詳しく書いた。2. 単位、定数
本論に入る前によく使う単位、定数を表1にまとめておく。本書では議論が抽象的にならぬよう、なるべく具体的な数値を使った概算を示す。読者には学んだことを使える知識として身につけてほしい。そのためにまず、よく使う単位、定数を押さえておこう。| 単位または定数 | 記号 | 値 | |
|---|---|---|---|
| フェムトメートル | \(\mathrm{fm}\) | 10\(^{-15} \;\mathrm{m}\) | |
| バーン | \(\mathrm{b}\) | 10\(^{-24} \;\mathrm{cm}^2\) | |
| 電子ボルト | \(\mathrm{eV}\) | \(1.60217663 \times 10^{-19} \;\mathrm{J}\) | |
| 素電荷 | \(e\) | \(1.60217663 \times 10^{-19} \;\mathrm{C}\) | |
| 光速 | \(c\) | \(2.99792458 \times 10^{8} \;\mathrm{m/s}\) | |
| プランク定数 | \(h\) | \(6.62607015 \times 10^{-34} \;\mathrm{J}\cdot \mathrm{s}\) | |
| \(\hbar\) | \(1.054571817 \times 10^{-34} \;\mathrm{J}\cdot \mathrm{s}\) | ||
| \(\hbar c\) | \(197 \;\mathrm{MeV}\cdot \mathrm{fm}\) | ||
| 微細構造定数 | \(\alpha\) | \(1/137.035999\) | |
| 陽子質量 | \(m_p\) | \(938.272 \;\mathrm{MeV}\) | |
| 中性子質量 | \(m_n\) | \(939.565 \;\mathrm{MeV}\) | |
| 電子質量 | \(m_e\) | \(0.510999 \;\mathrm{MeV}\) |
エネルギーの単位には、ジュールはほとんど使わない。代わりに電子ボルト(\(\mathrm{eV}\))を用いる。\(1\;\mathrm{eV}\)の定義は、1素電荷の粒子を1 \(\mathrm{V}\)の電位差で加速したときに粒子が得るエネルギーである。原子核の実験においては、加速器の電場で加速した粒子を用いるため、このような定義の単位は非常に便利である。MeV(\(10^6 \mathrm{eV}\))やkeV(\(10^3 \mathrm{eV}\))がよく用いられる。ちなみに定義から1 \(\mathrm{eV}\)をジュールで換算すると
\begin{align} 1 \;\mathrm{eV} = 1.602 \times 10^{-19} \;\mathrm{J} \end{align} である。
プランク定数は第1章で述べたように量子力学を特徴づける定数である。MKS単位系で
\begin{align} \hbar = \frac{h}{2\pi}=1.05457 \times 10^{-34} \mathrm{J}\cdot \mathrm{s} \end{align} という値となる。しかし、この単位は原子核物理の計算には使いづらい。そこで光速\(c\)を乗じて
\begin{align} \hbar c = 1.054 \times 10^{-34} \mathrm{J}\cdot \mathrm{s} \times 2.998 \times 10^{8} \mathrm{m/s} = 3.160 \times 10^{-26} \mathrm{J}\cdot \mathrm{m} \end{align} とし、これをMeV(\(1.602 \times 10^{-13}\)J)とfm(10\(^{-15}\) m)を使って換算すると \begin{align} \hbar c = 197 \;\mathrm{MeV}\cdot \mathrm{fm} \end{align} になる。本書で\(\hbar\)を含む計算では必ずこの値を用いる。ぜひ、\(\hbar c = 197 \;\mathrm{MeV}\cdot \mathrm{fm}\)という値は覚えてほしい注。
アインシュタインによりエネルギーと質量は等価であることが示された。エネルギーと質量の等価性は、おそらく物理学の中で最も有名な次の関係式で表される。
\begin{align} E &= mc^2 \tag{2.1} \end{align} ここで、\(E\)はエネルギー、\(m\)は静止質量、\(c\)は光速である。この式から質量はkgではなくエネルギーの単位(\(\mathrm{MeV}\))で表される。6節で述べるように反応前後の質量の変化が運動エネルギーとして放出(または吸収)されるため、質量をエネルギー単位で表現すると都合が良い。参考に陽子、中性子、電子の質量を表1に示す。
3. クーロン障壁
2つの原子核が接近し核力をおよぼし合うと原子核反応が起こり得る。原子核反応により原子核を構成する陽子や中性子の数が変わったり、エネルギーが放出されたりする。しかし、核力の到達距離は10\(^{-15}\)m程度と極めて短い。正の電荷を持つ原子核同士はクーロン斥力で反発しており、物質中ではお互い10\(^{-10}\)m程度の距離離れている。身の回りの物質中の原子核同士がクーロン力に打ち勝って核力の相互作用範囲内にまで接近し核反応が起こることはない。原子核同士をそこまで近づけるには、クーロン力に打ち勝つだけの十分な運動エネルギーが必要である。2つの原子核が接触するためにエネルギー的に越える必要のある電気的障壁をクーロン障壁という。クーロン障壁を超えるには物質を恒星内部のような高温状態にするか、もしくは加速器を用いて原子核を加速し運動エネルギーを与える必要がある。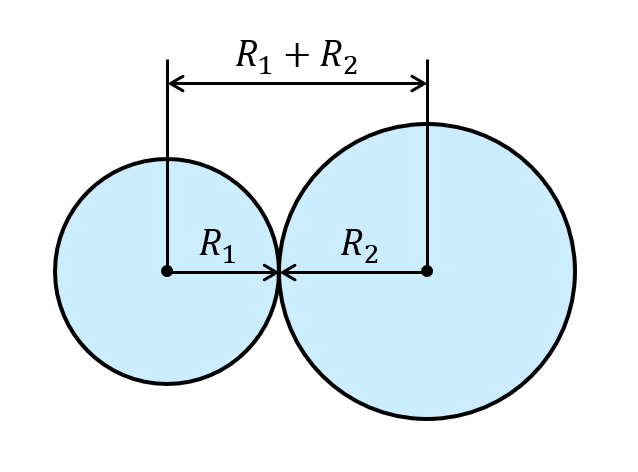
図1 2つの接近した原子核
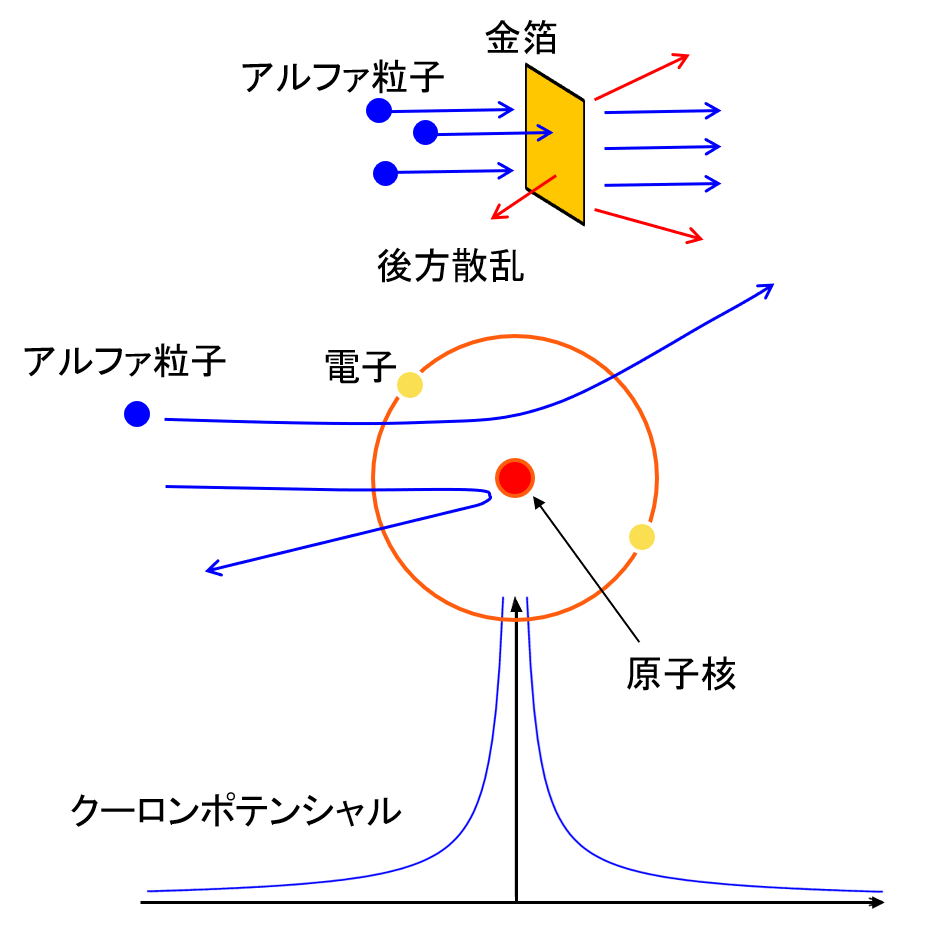
図2 ラザフォード散乱
式(2)を用いてラザフォードの考察について理解を深めてみよう。式(2)から\(\alpha\)(\(^4_2\)He)と金(\(^{197}_{79}\)Au)のクーロン障壁を計算する。\(\alpha\)と\(^{197}\)Auの半径は、\(R=r_0 A^{\frac{1}{3}}\)から計算するとそれぞれ1.9 fm, 7.0 fmとなる。これらを代入するとクーロン障壁は \begin{align} V(\alpha+^{197}\rm{Au}) &= 1.44\times\frac{2 \times 79}{1.9 + 7.0}=25.6\:[\rm{MeV}] \end{align} が得られる。ここでラジウム(\(^{226}\)Ra)から放出される\(\alpha\)線のエネルギーは4.8 MeVである。クーロン障壁25.6 MeVよりもずっと小さい。したがって、\(\alpha\)粒子は金の原子核のクーロン障壁を乗り越えることができず跳ね返される。これが後方散乱となって現れる。では、もし、原子の構造が当時の多くの物理学者が信じていたプディングモデルのようなものだったらどうなるか。プディングモデルは、正電荷を帯びた媒質中に多数の電子が埋め込まれている描像である。この場合、正電荷は原子全体に広がっている。したがって、典型的な原子サイズ10\(^{-10}\:\)m(10\(^{5}\:\)fm)を式(2)に代入してみると、クーロン障壁は、 \begin{align} 1.44\times\frac{2 \times 79}{10^5}=0.0023\:[\rm{MeV}]=2.3\:[\rm{keV}] \end{align} となる。この場合、クーロン障壁は、\(\alpha\)粒子のエネルギー4.8 MeVの約2000分の1であり、ないに等しい。後方散乱は起きようがなく、\(\alpha\)粒子はほとんど抵抗を受けず素通りするはずである。起きうる散乱は、せいぜい前方の小角散乱だけと予想される(したがって、当初の実験は前方にしか興味がなかった)。このことから後方散乱が観測されたときのラザフォードの驚きが実感できる。ラザフォードの言葉を借りれば、まさに「まるでピストルで紙きれを撃ったら弾丸がはね返ってきたと聞かされたような」驚きである文献。
実際には、この実験では\(\alpha\)粒子のエネルギーが低すぎるため原子核半径の上限のみが与えられる。どれくらいの距離まで\(\alpha\)粒子が接近できるか計算してみよう。計算するには、式(2)の左辺を\(\alpha\)粒子のエネルギーと等しいと置き、逆に距離を求めてやればよい。ここで距離を\(D\)とした。値を代入して計算すると \begin{align} 4.8\:[\rm{MeV}] &= 1.44\times\frac{Z_1 Z_2}{D} =1.44\times\frac{2 \times 79}{D}\\ \therefore\; & D = \frac{1.44\times2 \times 79}{4.8} = 48\:[\rm{fm}] \end{align} となり、原子核半径の上限値として48 fmが得られる。このことからラザフォードは、原子核は\(10^{-14}\) mより小さいと結論づけた注。
4. 中性子の特殊性
中性子は電荷を持たない中性粒子である。したがって、当然のことながら中性子にはクーロン力は働かず、クーロン障壁は存在しない。そのため、中性子の場合には上で述べた状況とは大きく異なってくる。クーロン障壁が存在しないため、中性子は運動エネルギーがいくら低くなっても相手の原子核に近づき核反応を起こすことができる。例えば、室温300 Kで熱平衡状態にある中性子(熱中性子)の平均エネルギーは25 meVであるが、この低いエネルギーでも中性子は原子核反応を起こす。このようなmeVという極めて低いエネルギーでの核反応は、陽子や\(\alpha\)粒子などの荷電粒子では到底考えられないことである。荷電粒子の場合、原子核反応を起こす下限のエネルギーは、中重核であればMeVオーダ、反応しやすいD(\(^2\)H)やT(\(^3\)H)などの軽核でもkeVオーダで、それより低いエネルギーでは核反応は起こらない。原子力工学において中性子核反応は特に重要である。これは原子炉が中性子核反応を動力源にしていることを考えれば当たり前のことである。原子炉中には、核分裂から放出されるMeVオーダの高速中性子から減速材で熱化した熱中性子まで様々なエネルギーの中性子が存在する。したがって、工学的な応用の観点からmeVからMeVまでの10桁ほどの幅広い中性子エネルギーに渡って中性子核反応断面積のデータが必要とされる。
5. 原子核反応の表記法

図3 核反応の表記法
その他いくつかの決まりを以下にまとめる。ただし、あくまで一般的なルールであり、これらに従っていない場合もある。
- 括弧内の入射粒子、放出粒子が、陽子、重陽子、三重陽子の場合は、元素記号は使わずにそれぞれ小文字で\(p\), \(d\), \(t\)で表す。それより重い原子核を括弧内に書く場合には、標的核と同様に元素記号と質量数の組み合わせでよい。
- 括弧内の\(\alpha\)粒子、中性子、\(\gamma\)線は、\(\alpha\), \(n\), \(\gamma\)で表す。
- 括弧外の標的核、残留核は、元素記号の左上に質量数をつけて表す。例:\(^{11}\rm{Be}\)(\(p,n\))\(^{11}\rm{B}\)
- 残留核が励起される場合には、残留核の右上にアスタリスク\(*\)をつける。例:\(^{10}\rm{B}\)\((n,\alpha)\)\(^7\rm{Li}^*\)
- 非弾性散乱の場合、放出粒子に\(\:'\:\)をつける。例:\(^{12}\rm{C}\)\((p,p')\)\(^{12}\rm{C}^*\)
- 終状態が3体の場合(すなわち放出粒子2個+残留核)、括弧内の放出粒子として2つ書く。\(2n\)は中性子が2個の意。
例:\(^{90}\rm{Zr}\)\((p,pn)\)\(^{89}\rm{Y}\), \(^{65}\rm{Zn}\)\((p,2n)\)\(^{64}\rm{Ga}\) - 核分裂の場合、\(f\:\)で表す。例:\(^{235}\rm{U}\)\((n,f)\)
- 残留核が入射粒子、標的核、放出粒子の組み合わせから自明の場合、しばしば省略する。
6. 反応のQ値
原子核反応によりエネルギーが放出されたり、吸収されたりする。\(\rm{X}\)\((a,b)\)\(\rm{Y}\)反応について、次式で定義される反応後の運動エネルギーの総和\(K_b + K_\mathrm{Y}\)から反応前の運動エネルギーの総和\(K_a + K_\mathrm{X}\)を引いたものをQ値と呼ぶ。 \begin{align} Q &= (K_b + K_\mathrm{Y}) - (K_a + K_\mathrm{X}) \\ &= K_b + K_\mathrm{Y} - K_a - K_\mathrm{X} \tag{2.3}\\ &= \frac{1}{2}m_b v_b^2 + \frac{1}{2}m_\mathrm{Y} v_\mathrm{Y}^2 - \frac{1}{2}m_a v_a^2 - \frac{1}{2}m_\mathrm{X} v_\mathrm{X}^2 \end{align} ここで、\(m_a, m_\mathrm{X}, m_b, m_\mathrm{Y}\)は、それぞれの粒子の静止質量、\(v_a, v_\mathrm{X}, v_b, v_\mathrm{Y}\)は速さである。式(3)の定義から\(Q\)が正の時、反応後の運動エネルギーの総和\(\frac{1}{2}m_b v_b^2 + \frac{1}{2}m_\mathrm{Y} v_\mathrm{Y}^2\)の方が、反応前の総和\(\frac{1}{2}m_a v_a^2 + \frac{1}{2}m_\mathrm{X} v_\mathrm{X}^2\)より大きくなる。つまり、発熱反応である。逆に\(Q\)が負の時、反応後のエネルギーの総和は反応前より小さくなり、吸熱反応となる。
ところで、この反応前後の運動エネルギーの差はどこから生じているのだろうか。それは原子核内部の結合エネルギーの変化から生じている。結合エネルギーとは、原子核をばらばらにして一つ一つの陽子と中性子にするのに要するエネルギーである。例えば、重陽子は陽子1個、中性子1個からなる一番単純な原子核であるが、その結合エネルギーは2.22 MeVである。つまり、重陽子を陽子と中性子に分解するのに2.22 MeVのエネルギーが必要となる。逆に言えば、陽子と中性子が結合せずばらばらでいるより重陽子として結合するほうが2.22 MeVだけエネルギー的に低い状態になる(だから結合している)。結合エネルギーが大きいほど結合が強く内部エネルギーが低い。つまりエネルギー的に安定である。したがって、反応後に、より大きい結合エネルギーの原子核になれば、その余剰分が運動エネルギーとして放出される。これがQ値である。
もう少し具体的に見てみよう。例として重陽子2個から中性子と\(^3\mathrm{He}\)が生成される以下の反応 \(^2\mathrm{H}(d,n)^3\mathrm{He}\)を取り上げる。 \begin{align} d + d & \rightarrow n + ^3\mathrm{He} \end{align}
重陽子の1個の結合エネルギーは上で述べたように2.22 MeVである。一方、\(^3\mathrm{He}\)の結合エネルギーは7.72 MeVである。陽子2個と中性子2個が結合していないバラバラの状態をエネルギーの基準として\(0\)とすると重陽子と\(^3\mathrm{He}\)はエネルギー的にそれぞれ2.22 MeVと7.72 MeV低い状態となる(図4)。\(^2\mathrm{H}(d,n)^3\mathrm{He}\)反応において反応前後のエネルギー変化を計算するには\(^3\mathrm{He}\)の束縛エネルギーから重陽子2個分の束縛エネルギーを引いてやればよい(反応後の単体の中性子は結合していないので計算から除外できる)。すなわち \begin{align} (反応前後のエネルギー変化) &= (反応後\; ^3\mathrm{He}) - (反応前\; d \times 2個)\\ &= 7.72 - 2.22 \times 2\\ &=3.28\; \mathrm{MeV} \end{align} が得られる。つまり、反応後の方が、エネルギーが3.28 MeVだけ低くなる。この余剰分3.28MeVがQ値であり、放出粒子である中性子と\(^3\mathrm{He}\)の運動エネルギーとなる。
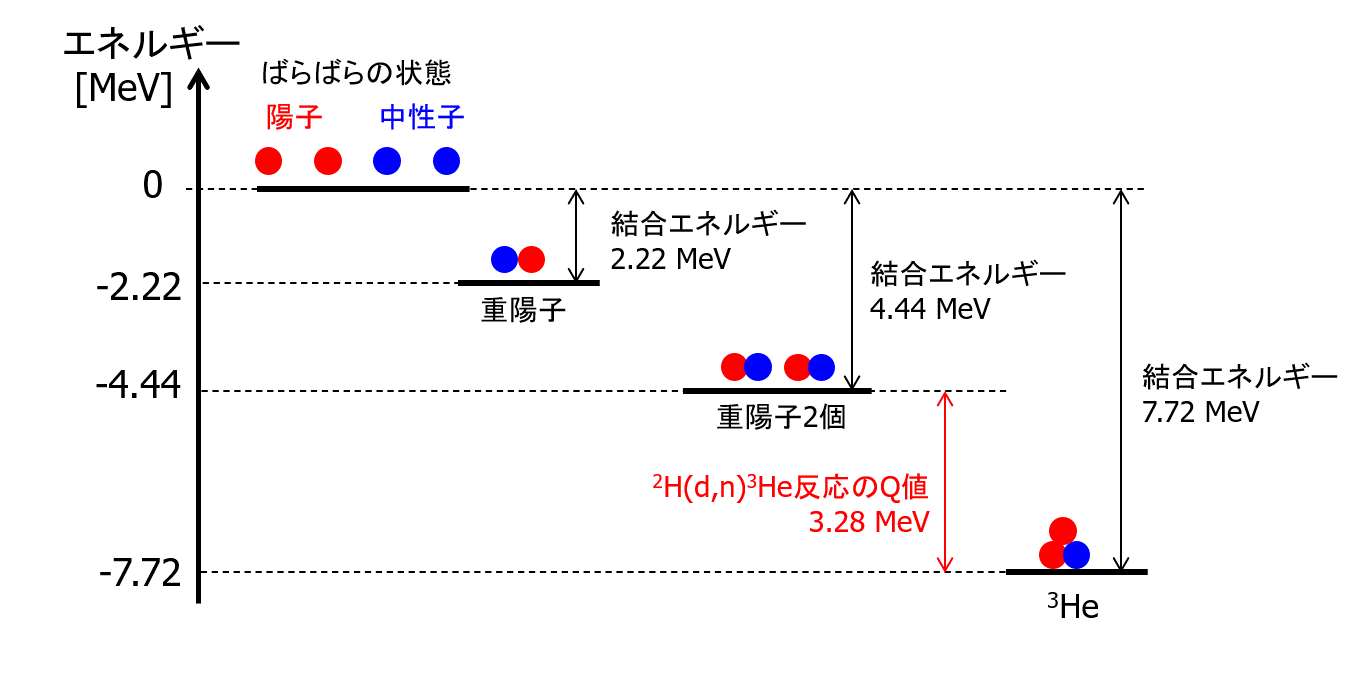
図4 重陽子と\(^3\mathrm{He}\)の結合エネルギーと\(^2\mathrm{H}(d,n)^3\mathrm{He}\)反応のQ値
ここで束縛エネルギーと質量の関係について触れる。アインシュタインによりエネルギーと質量は等価であることが示された。エネルギーと質量の等価性は、おそらく物理学の中で最も有名な次の関係式で表される。 \begin{align} E &= mc^2 \tag{2.4} \end{align} ここで、\(E\)はエネルギー、\(m\)は静止質量、\(c\)は光速である。
この式に従えば、結合の結果、より低いエネルギー状態となれば、その結合エネルギー分だけ質量が軽くなる。これを質量欠損という。上記の例でいえば、重陽子の結合エネルギーは2.22MeVなので、陽子と中性子がばらばらでいるよりも2.22MeVだけ軽くなる。陽子、中性子、重陽子の静止質量をそれぞれ\(m_p, m_n, m_d\)とすると \begin{align} m_d &= m_p + m_n -2.22 \;\mathrm{MeV} \end{align} となる。この質量変化は大きいのだろうか。小さいのだろうか。陽子と中性子の質量はそれぞれ938.3 MeV、939.6 MeVなので、その和は、1877.9 MeVである。重陽子の質量はこの和よりも2.22 MeVだけ小さい。したがって、約0.1%の質量減少である。この質量変化は一見小さく見えるが、十分観測可能な大きさである。実際のところ、原子核の黎明期において、原子核の結合エネルギーは、式(4)のおかげで質量の精密測定から判明した。放射線検出技術が未発達だった当時でも磁場を用いた質量分析は可能だったからである。
ちなみにしばしば誤解されていることだが、結合による質量減少は原子核に限らない。式(4)は、核力に限らず、あらゆる相互作用について一般的に成り立つ関係である。ただ、質量変化の程度が異なるだけである。例えば、化学的な結合の例として水素原子を考えてみよう。水素原子は、陽子と電子がクーロン力で結合している。電子が基底状態にあるときの束縛エネルギーは、13.6 eVである。つまり、水素原子はばらばらの陽子と電子より13.6 eVだけ軽くなる。この質量減少は陽子質量938.3 MeVと電子質量0.511 MeVの和938.8 MeVに対し\(10^{-8}\)程度であり極めて小さい。このことから、いかに原子核の結合エネルギーが大きいかが分かるだろう。
さて、ここでQ値を実際に計算する方法について説明する。\(^2\mathrm{H}(d,n)^3\mathrm{He}\)反応の例で計算したように反応前と反応後の結合エネルギーの差がQ値である。一方、エネルギーと質量の等価性から結合エネルギーは質量欠損として原子核質量に反映される。したがって、反応前後の質量の変化からも反応のQ値を計算することができる。すなわち、\(\rm{X}\)\((a,b)\)\(\rm{Y}\)反応において、粒子質量をそれぞれ\(m_\mathrm{X}, m_a, m_b, m_\mathrm{Y}\)とすると反応のQ値は \begin{align} Q &= (m_a c^2 + m_\mathrm{X} c^2) - (m_b c^2 + m_\mathrm{Y} c^2) \tag{2.5} \end{align} となる。
原子質量は基本的かつ重要な核データであり、データベースとしてよく整備されている。したがって、データベースに整備された原子質量を用いることで式(5)からQ値が計算される。Q値の計算にはQ value calculatorなどの便利なツールがインターネット上に提供されており、これらを用いれば簡単に計算することができる。
7. さまざまな原子核反応とQ値
| 原子核反応 | Q値 (MeV) | ||
|---|---|---|---|
| 軽核の核融合反応 | |||
| 2H(d,n)3He | \(d + d \rightarrow n + ^3\mathrm{He}\) | 3.27 | |
| 3He(n,p)3H | \(n + ^3\mathrm{He} \rightarrow p + ^3\mathrm{H}\) | 0.764 | |
| 3H(d,n)4He | \(d + t \rightarrow n + \alpha\) | 17.59 | |
| 3He(d,p)4He | \(d + ^3\mathrm{He} \rightarrow p + \alpha\) | 18.35 | |
| 中性子捕獲反応 | |||
| 1H(n,\(\gamma\))2H | \(p + n \rightarrow d + \gamma\) | 2.22 | |
| 56Fe(n,\(\gamma\))57Fe | \(n + ^{56}\mathrm{Fe} \rightarrow \; ^{57}\mathrm{Fe} + \gamma\) | 4.95 | |
| 238U(n,\(\gamma\))239U | \(n + ^{238}\mathrm{U} \rightarrow \; ^{239}\mathrm{U} + \gamma\) | 4.81 | |
| Q値が負の反応 | |||
| 7Li(p,p')7Li* | \(p + ^{7}\mathrm{Li} \rightarrow \; p + ^{7}\mathrm{Li^*}\) | -0.478 | |
| 7Li(p,n)7Be | \(p + ^{7}\mathrm{Li} \rightarrow \; n + ^{7}\mathrm{Be}\) | -1.64 | |
| 9Be(p,n)9B | \(p + ^{9}\mathrm{Be} \rightarrow \; n + ^{9}\mathrm{B}\) | -1.85 | |
| 2H(\(\gamma\),n)1H | \(d + \gamma \rightarrow p + n \) | -2.22 | |
| 核分裂反応 | |||
| U, Pu, Thなど | \(\rightarrow\) F.P. + F.P. + n + ... | \(\sim \) 200 |
(核融合反応)軽い原子核の核融合反応はQ値が正のものが多い。クーロン障壁が低いために反応が起きやすく将来のエネルギー源として期待されてきた。特に3H(d,n)4He反応は現在開発が進められている核融合炉のエネルギー源である。Q値が17.59 MeVと非常に大きい。3He(n,p)3H反応は、3He比例計数管などの中性子検出器でよく使われている反応である。
(中性子捕獲反応)中性子捕獲反応は、入射中性子が標的原子核に取り込まれその一部となる反応である。反応後、中性子や陽子などの粒子は出てこない。ただし、中性子を吸収後、原子核は高い励起状態にあるため、その励起エネルギーをガンマ線の形で放出する。したがって、中性子捕獲反応は(n,\(\gamma\))とも書かれる。中性子捕獲反応は安定核近傍ではほぼ全ての原子核が起こすと考えてよい。
(非弾性散乱)Q値が負の反応の例として、まず非弾性散乱7Li(p,p')7Liを挙げた。非弾性散乱では入射粒子と放出粒子は変わらないが、標的原子核を励起状態にする。この例だと7Liを励起エネルギー0.478 MeVの第1励起準位に励起する注。入射陽子の運動エネルギーが7Liの励起に用いられる。したがって、Q値は、-0.478 MeVである。
((p,n)反応)安定核種近傍では、多くの核種で(p,n)反応のQ値は負である。例として7Li(p,n)7Be反応と9Be(p,n)9B反応を挙げた。これらの反応は加速器中性子源の中性子発生反応としてよく使われている。
(ガンマ線入射反応)2H(\(\gamma\),n)1H反応は、ガンマ線入射反応である。ガンマ線が重陽子と反応し、重陽子を陽子と中性子に分解する。光分解反応とも呼ばれる。よく見ると1H(n,\(\gamma\))2H反応の逆反応になっていることが分かる。逆反応なのでQ値は1H(n,\(\gamma\))2HのQ値の符号を逆にしたもの、すなわち-2.22 MeVである。
(核分裂反応)核分裂はウランなどの重い原子核が2つに分裂する現象である。2つの核分裂生成物(fission products)と複数個の中性子が放出される。Q値は桁違いに大きく約200 MeVである。このQ値が原子力発電の源となっている。
8. 断面積
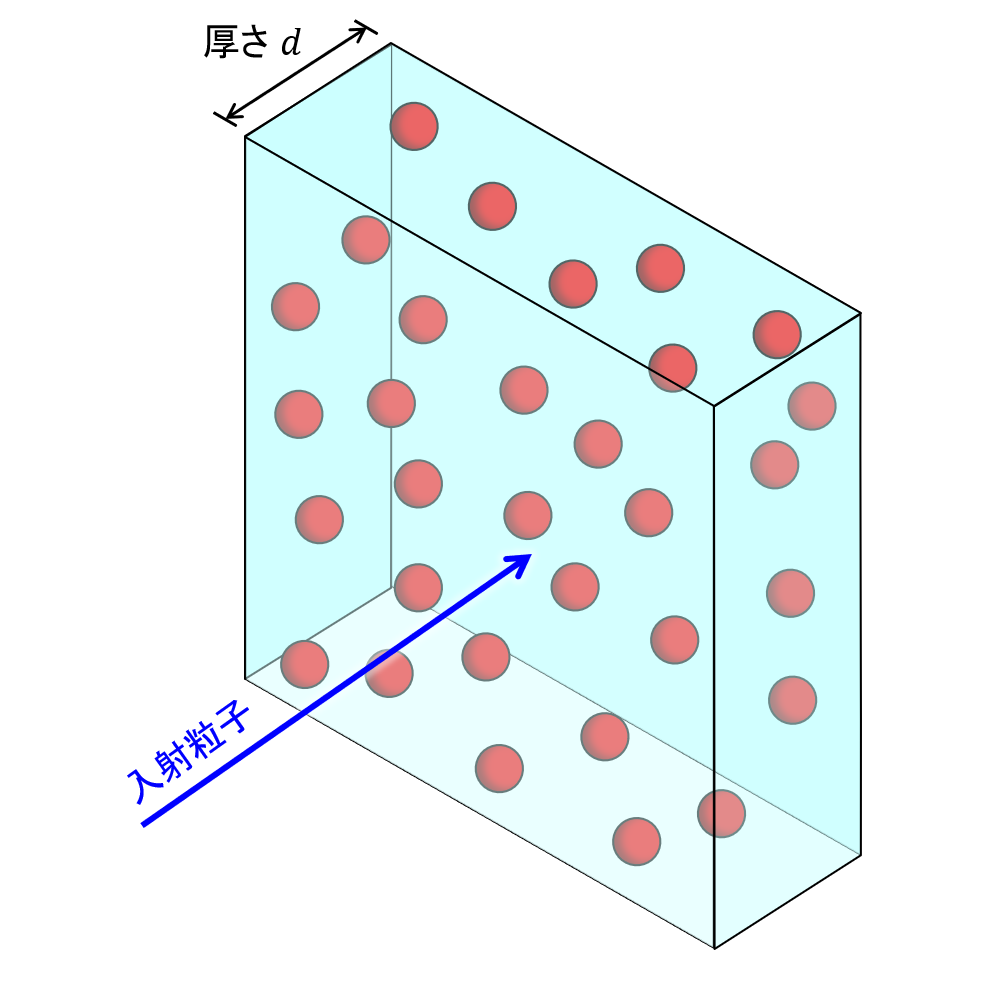
図5 平板内に均一に分布した小球
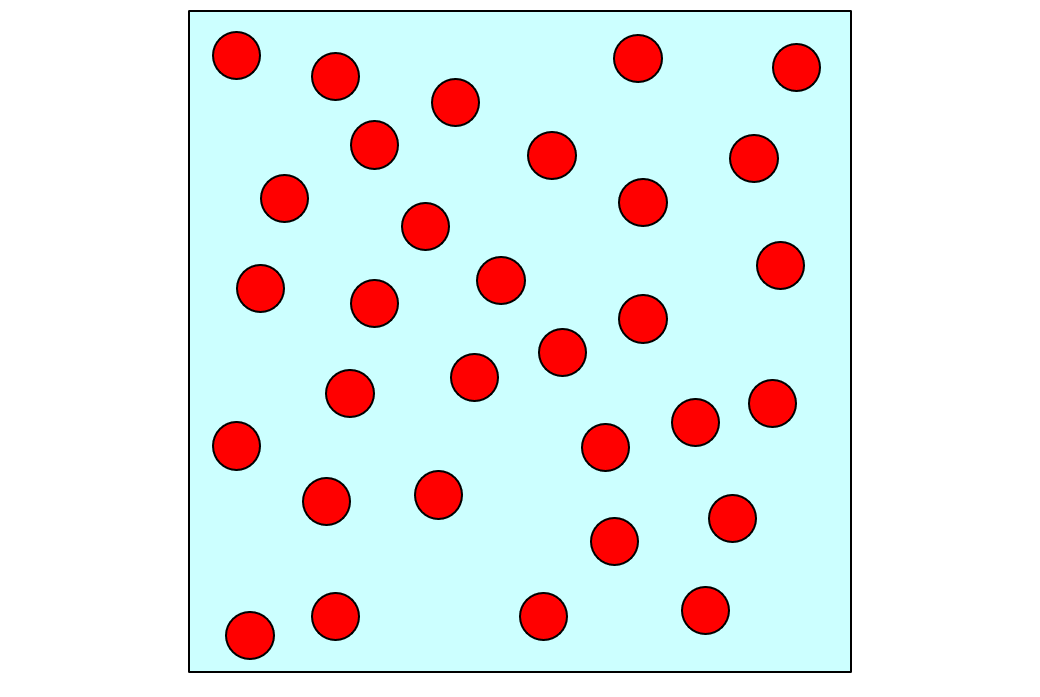
図6 入射粒子方向から見た図
式(6)を簡単な模型から導いてみよう。図5のように平板状の領域に半径\(r\)の小球が数密度\(N\)で均一にランダムに分布し、平板の垂直方向から入射粒子が飛んでくるとする。このとき、入射粒子が小球に当たる確率はいくつになるだろうか。平板の正面から見ると小球はの図6のように分布しているように見える。したがって、図6の平面内に小球の占める面積の割合を計算すれば入射粒子の当たる確率が求まる。入射粒子方向から見たときに小球同士の重なりがないとすれば、小球の数密度\(N\)に平板の厚さ\(d\)を乗じたもの\(Nd\)が、入射粒子方向から見た小球の面密度となる。この面密度に小球1個あたりの断面積\(\pi r^2\)を乗じてやれば小球が占める面積の総和が求まる。したがって、入射粒子が小球に当たる確率\(P\)は、 \begin{align} P &= N \times d \times \pi r^2 = N d \sigma \tag{2.7} \end{align} と書ける。ここで、小球の断面積\(\pi r^2\)を\(\sigma\)とおいた。さらに\(n\)個の粒子が入射して小球に当たった回数を\(Y\)とすれば、 \begin{align} Y = n P = n N d \sigma \end{align} となる。これで式(6)が得られた。以上の議論は、原子核の古典的なサイズを仮定して計算する場合に相当する。実際には量子力学的な効果があり、断面積の大きさは古典的なサイズとは異なってくるが、反応回数と断面積の関係式は変わらない。
では、実際の断面積の大きさはどれくらいなのだろうか。原子核の半径から断面積を計算してみよう。古典的な計算ではあるが、大きさの目安にはなる。例えば、金(\(^{197}\)Au)の原子核半径は、\(R=r_0 A^{\frac{1}{3}}\)から計算すると7.0 fmである。したがって、断面積は、 \begin{align} \pi R^2 = 3.14 \times (7.0 \times 10^{-13} \mathrm{cm})^2 =1.5 \times 10^{-24} \mathrm{cm^2} \end{align} となる注。この計算から分かるように断面積は、\(10^{-24}\) cm\(^2\)程度と極めて小さい。そこで断面積を表す単位としてバーン(barn, b)を用いる。1 barnは、\(10^{-24}\) cm\(^2\)である。したがって、上記の計算結果は、1.5 barnと表される。
ここで1.5 barnという結果を使って式(7)から入射粒子が原子核に当たるのはどれくらいの確率になるのか計算してみよう。例として、MeVオーダーの陽子が貫通できる厚さということで10 \(\mu\)mの金箔を想定する。原子数密度は比重\(\rho\)を原子量\(A\)で割り、アボガドロ定数\(N_A\)をかけることで求められる。金の比重は19.3 g/cm\(^3\)、原子量は197である。したがって、入射粒子が金の原子核に当たる確率は \begin{align} P &= N d \sigma = \frac{\rho \times N_A \times d \times \sigma}{A} = \frac{19.3 \times 6.02 \times 10^{23} \times 1 \times 10^{-4} \times 1.5 \times 10^{-24}}{197}=0.88 \times 10^{-5} \end{align} となる。だいたい\(10^{-5}\)のオーダー、すなわち10万分の1くらいの確率でしか反応は起こらない。この計算から極めて小さい数字であることが分かるだろう。このことから、式(7)を導出した議論において、小球同士の重なりはないとした仮定は妥当であることが分かる。なぜなら、原子核が占めている面積割合は10万分の1程度であり重なり合う確率は極めて小さいからである注。
(面密度)式(6)の中では厚さ\(d\)と原子数密度\(d\)は、その積\(Nd\)の形で現れるため、計算には\(Nd\)が与えられていれば十分である。\(Nd\)は原子数面密度である。原子核反応の観点から言えば、物理的な厚さ\(d\)よりもこの原子数面密度\(Nd\)の方がより本質的である。なぜなら、入射粒子の経路上に何個の原子核が存在しているかが反応回数を決めるからである。また、実験的にも原子数面密度の方が扱いやすい。薄膜の物理的な厚さを精密に測定するのは容易ではないが、面密度であれば、試料の重さを測り、その重量を試料面積で割ってやれば面密度は簡単に求まるからである。そのため、g/cm\(^2\)やmg/cm\(^2\)で表した質量面密度を単に「厚さ」と呼ぶことも多い。
(厚い標的と自己遮蔽)式(6)は標的物質が十分に薄い場合の式である。そのため標的が厚くなるとこのままでは適用できない。物質表面からの深さに応じて入射粒子数が反応により減少するからである。飛程の短い荷電粒子の場合にはあまり問題にはならないが、透過力の高い中性子の場合には特に重要である。そこで厚い標的物質に対する公式を求めてみよう。
表面からの深さ\(x\)での入射粒子の数を\(n(x)\)とする。微小厚さ\(\Delta x\)中で反応する入射粒子の数は、\(n(x) N \sigma dx\)であり、この分だけ入射粒子は減少する。微分方程式で書くと \begin{align} \Delta n(x) &= - n(x) N \sigma \Delta x \\ \therefore\; \frac{dn(x)}{dx} &= - N \sigma n(x) \end{align} となる。これを解くと \begin{align} n(x) &= n_0 \exp(-N \sigma x) \tag{2.8} \end{align} が得られる。ここで\(n_0\)は物質表面での入射粒子数である。厚さ\(d\)の物質での反応回数\(Y\)は、入射粒子数の減少分に等しいので \begin{align} Y = n_0 - n(d) = n_0(1- \exp(-N d \sigma)) \tag{2.9} \end{align} となる。この式から分かるように反応回数は標的厚さに比例せず、\(n_0\)を上限として飽和する。これを自己遮蔽と呼ぶ。
(巨視的断面積)原子炉物理においては、以下の式に示すように\(\sigma\)に原子数密度\(N\)を乗じた巨視的断面積\(\Sigma\)がよく用いられる。また、断面積を混同しないために\(\sigma\)は微視的断面積とも呼ばれる。 \begin{align} \Sigma &= N \sigma \tag{2.10} \end{align} 原子炉物理では、原子炉という物理的に大きな体系の中を中性子がランダムに飛び交う状況を扱う。上の議論で扱った一方向から薄い物質に入射する単純な体系とは大きく異なる。式(9)のように密度を予め乗じた巨視的断面積の形にするほうが計算上便利である。巨視的断面積を使うと式(8)も簡単になって \begin{align} n(x) &= n_0 \exp(-\Sigma x) \tag{2.11} \end{align} となる。
(角分布、微分断面積)
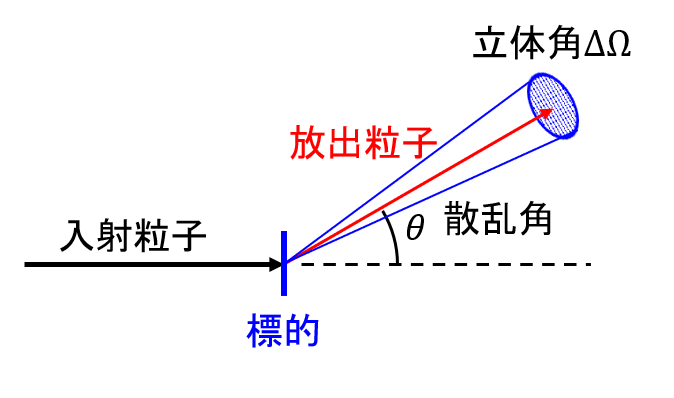
図7 放出粒子と散乱角
9. 原子核反応の運動学注
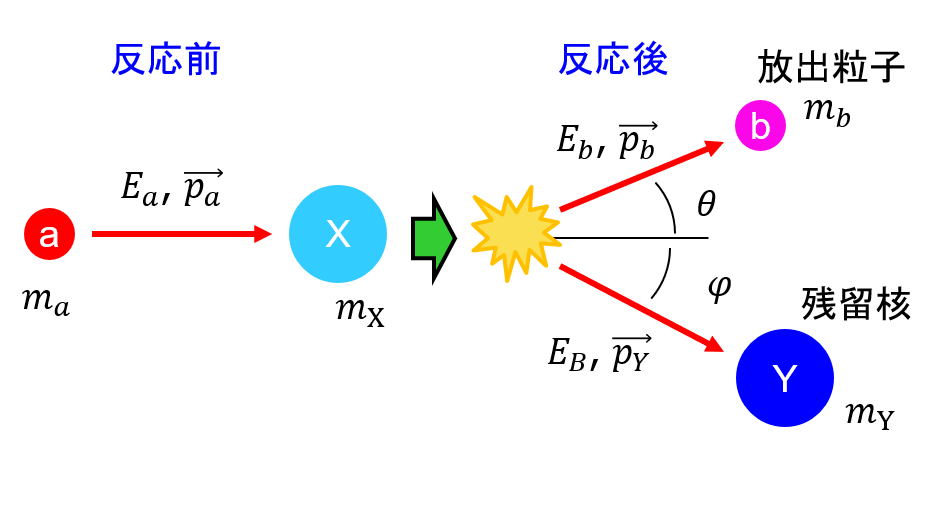
図8 原子核反応の運動学
式(13)を入射粒子の運動量に平行な成分と垂直な成分に分解すると \begin{align} p_a &= p_b \cos \theta + p_Y \cos \varphi \tag{2.15}\\ 0 &= p_b \sin \theta - p_Y \sin \varphi \tag{2.16} \end{align} となる。
粒子\(a, b, Y\)の質量をそれぞれ\(m_a, m_b, m_Y\)とすると \begin{align} E_a = \frac{p_a^2}{2 m_a},\; E_b = \frac{p_b^2}{2 m_b},\; E_Y = \frac{p_Y^2}{2 m_Y} \end{align} となり、式((14)は、 \begin{align} \frac{p_a^2}{2 m_a} &= \frac{p_b^2}{2 m_b} + \frac{p_Y^2}{2 m_Y} +Q \tag{2.17} \end{align} となる。
式(15)(16)(17)を連立して解くことで散乱角\(\theta\)に対する放出粒子の運動量\(p_b\)(もしくは速さ\(v_b\))を求めることができる。

図9 実験室系と重心系
実験室系から重心系への変換はガリレイ変換によって行う。図9から分かるように変換ベクトルとして入射粒子と反対方向の速度ベクトル\(\boldsymbol{u_X}\)を加えてやればよい。\(\boldsymbol{u_X}\)は標的核の重心系での速度ベクトルそのものである。実験室系での入射粒子の速さを\(v_a\)とすると、重心系での速さ\(u_a, u_X\)は、\(v_a\)を\(m_X : m_a\)で分割したものなので、 \begin{align} \boldsymbol{u_a} &= \frac{m_X}{m_a + m_X}\boldsymbol{v_a} \tag{2.22}\\ \boldsymbol{u_X} &= -\frac{m_a}{m_a + m_X}\boldsymbol{v_a} \tag{2.23}\\ \boldsymbol{V_T}&=\boldsymbol{u_X} \tag{2.24} \end{align} となる。ここで\(\boldsymbol{V_T}\)は変換ベクトルである。

図10 重心系の運動量
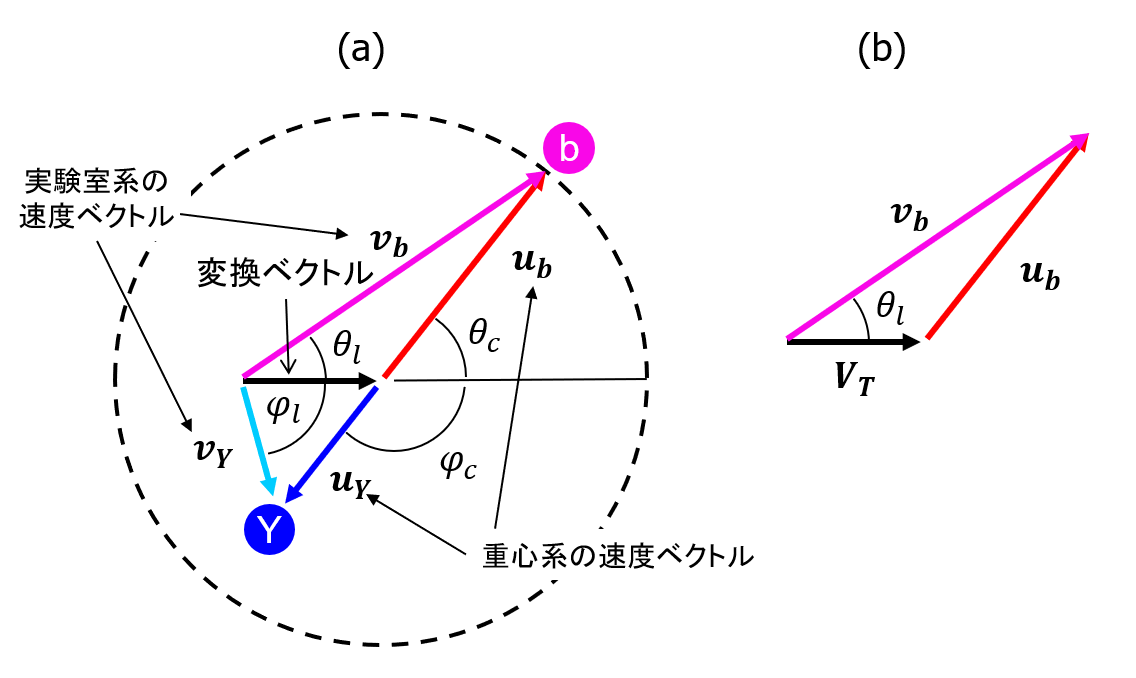
図11 反応後の重心系から実験室系への変換
\begin{align} u_b^2 = v_b^2 + V_T^2 - 2 v_b V_T \cos \theta_l \tag{2.27} \end{align} となる。これを\(v_b\)について解けば、
\begin{align} v_b^2 &- 2 v_b V_T \cos \theta_l - u_b^2 + V_T^2 =0\tag{2.28} \\ \therefore v_b &= V_T \cos \theta_l + \sqrt{V_T^2 \cos^2 \theta_l + u_b^2 - V_T^2}\\ & = V_T \cos \theta_l + \sqrt{u_b^2 - V_T^2 \sin^2 \theta_l} \tag{2.29} \end{align} となり、実験室系の速さ\(v_b\)が実験室系の散乱角\(\theta_l\)の関数として求まる注。
また、運動エネルギー\(E_b\)は
\begin{align} E_b = \frac{1}{2} m_b v_b^2 = \frac{1}{2} m_b \left(V_T \cos \theta_l + \sqrt{u_b^2 - V_T^2 \sin^2 \theta_l}\right)^2 \tag{2.30} \end{align} となる。
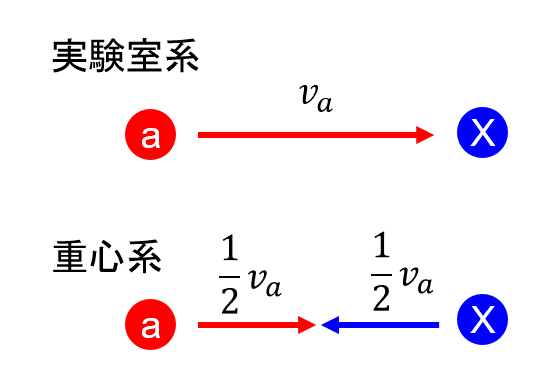
図12質量が等しい粒子の弾性散乱
計算の手順として、まず、実験室系から重心系に系を変換し、重心系で計算を行い、その結果を実験室系に変換する。このような手順を取る理由は重心系はいろいろな計算が簡単になる性質を持っているからである。
入射粒子と標的核の質量が等しいのでともに\(m\)とし、実験室系の入射粒子のエネルギーを\(E_{lab}\)とすると\(v_a\)は \begin{align} &E_{lab} = \frac{1}{2}m v_a^2 \\ &\therefore v_a = \sqrt{\frac{2E_{lab}}{m}} \tag{2.31} \end{align}

図13質量が等しい粒子の弾性散乱の
重心系から実験室系への変換
\begin{align} u_a = u_X = u_b = u_Y = \frac{1}{2}v_a \tag{2.35} \end{align} となる。図13に示すように散乱後の粒子の速度ベクトルは、半径\(u_a\)の円を描く。重心系から実験室系の変換は図13に示すように変換ベクトル\(\boldsymbol{V_T}=-\frac{1}{2}\boldsymbol{v_a}\)をたすと求めることができる。
図14に重心系でさまざまな角度に散乱された場合の実験室系への変換を示す。図14からわかるように重心系で\(90^{\circ}\)より大きい後方に散乱された場合でも実験室系では前方角度になることがわかる。これは変換ベクトルの大きさが重心系での粒子の速度ベクトルの大きさと同じため起こる現象である。図14からわかるように実験室系での最大角度は\(90^{\circ}\)である。 散乱後のエネルギーは式(30)で
\begin{align} V_T = u_b = u_a = \frac{1}{2}v_a \tag{2.36} \end{align} とすれば求めることができる。すなわち
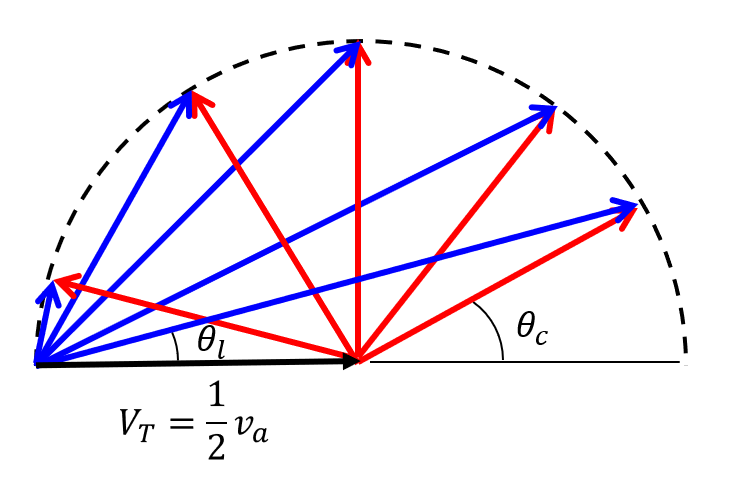
図14 質量が等しい粒子の弾性散乱。
さまざまな散乱角度の実験室系への変換
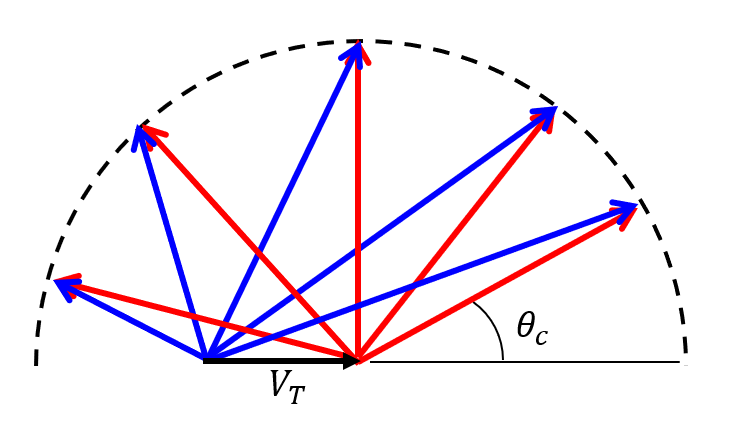
図15 一般的な弾性散乱(\(m_a < m_X\))。
さまざまな散乱角度の実験室系への変換
\begin{align} u_b & =u_a = \frac{m_X}{m_a + m_X}v_a \tag{2.38}\\ V_T & =u_X = \frac{m_a}{m_a + m_X}v_a \tag{2.39} \end{align} ここで、入射粒子が標的粒子よりも軽い(\(m_a < m_X\))としたので以下が成り立つ。
\begin{align} u_b < V_T \end{align} したがって、等しい質量の粒子同士の弾性散乱とは異なり、図15に示すように実験室系においても後方への散乱が起こる。
(発熱反応と吸熱反応)Q値がゼロではない反応の場合には、反応の前後で運動エネルギーの総和が変化する。重心系でのエネルギー保存則の式は次のようになる。
\begin{align} \frac{1}{2}m_a u_a^2 + \frac{1}{2}m_X u_X^2 + Q = \frac{1}{2}m_b u_b^2 + \frac{1}{2}m_Y u_Y^2 \tag{2.40}\\ \end{align} ただし、式(2.25)の重心系で運動量のベクトル和がゼロになるという条件は変わらない。すなわち \begin{align} \boldsymbol{p'_a} + \boldsymbol{p'_X} = \boldsymbol{p'_b} + \boldsymbol{p'_Y} = 0 \tag{2.41} \end{align} である。したがって、重心系において弾性散乱との違いは、放出粒子の速さ\(u_b\)が変化する(\(u_b \neq u_a\))ことだけである。重心系から実験室系への変換の仕方は変わらない。
図16に\(Q \neq 0\)の場合の重心系から実験室系へ変換のベクトル図を示す。発熱反応(\(Q > 0\))の場合(図16(a))には\(u_b\)は入射粒子の速さ\(u_a\)より大きくなる。重心系において放出粒子の速度ベクトルは角度によらず一定である。重心系から実験室系への変換は、弾性散乱と同様に変換ベクトル\(\boldsymbol{V_T}\)とのベクトル和をとればよい。吸熱反応(\(Q < 0\))の場合(図16(b))には、\(u_b\)は入射粒子の速さ\(u_a\)より小さくなる。それ以外の計算は同じである。
したがって、\(u_b\)を求めればよい。式(2.41)から
\begin{align} m_a u_a &= m_X u_X \tag{2.42}\\ m_b u_b &= m_Y u_Y \tag{2.43} \end{align} である。したがって、
\begin{align} u_X &= \frac{m_a}{m_X} u_a \tag{2.44}\\ u_Y &= \frac{m_b}{m_Y} u_b \tag{2.45} \end{align} 式(2.40)は次のように書き直せる。
\begin{align} &\frac{1}{2}m_a u_a^2 + \frac{1}{2}\frac{m_a^2}{m_X} u_a^2 + Q = \frac{1}{2}m_b u_b^2 + \frac{1}{2}\frac{m_b^2}{m_Y} u_b^2\\ &\therefore \frac{1}{2}m_a\left(\frac{m_a+m_X}{m_X} \right) u_a^2 + Q = \frac{1}{2}\left(m_b + \frac{m_b^2}{m_Y}\right) u_b^2 \tag{2.46}\\ \end{align} ここで\(u_a^2\)を実験室系の速さ\(v_a\)に直し、さらに入射エネルギー\(E_{lab}\)で表すと
\begin{align} u_a^2 = \frac{m_X^2}{(m_a + m_X)^2} v_a^2 = \frac{m_X^2}{(m_a + m_X)^2} \frac{2 E_{lab}}{m_a} \tag{2.47} \end{align} となる。これを式(2.46)に代入してやると\(u_b\)が次のようにもとまる。
\begin{align} & \left(\frac{m_X}{m_a+m_X} \right) E_{lab} + Q = \frac{1}{2}m_b\left(\frac{m_b+m_Y}{m_Y}\right) u_b^2 \\ & \therefore u_b = \sqrt{\frac{2}{m_b}\left(\frac{m_Y}{m_b+m_Y}\right)\left(\frac{m_X E_{lab}}{m_a+m_X} + Q\right) } \tag{2.48} \end{align}
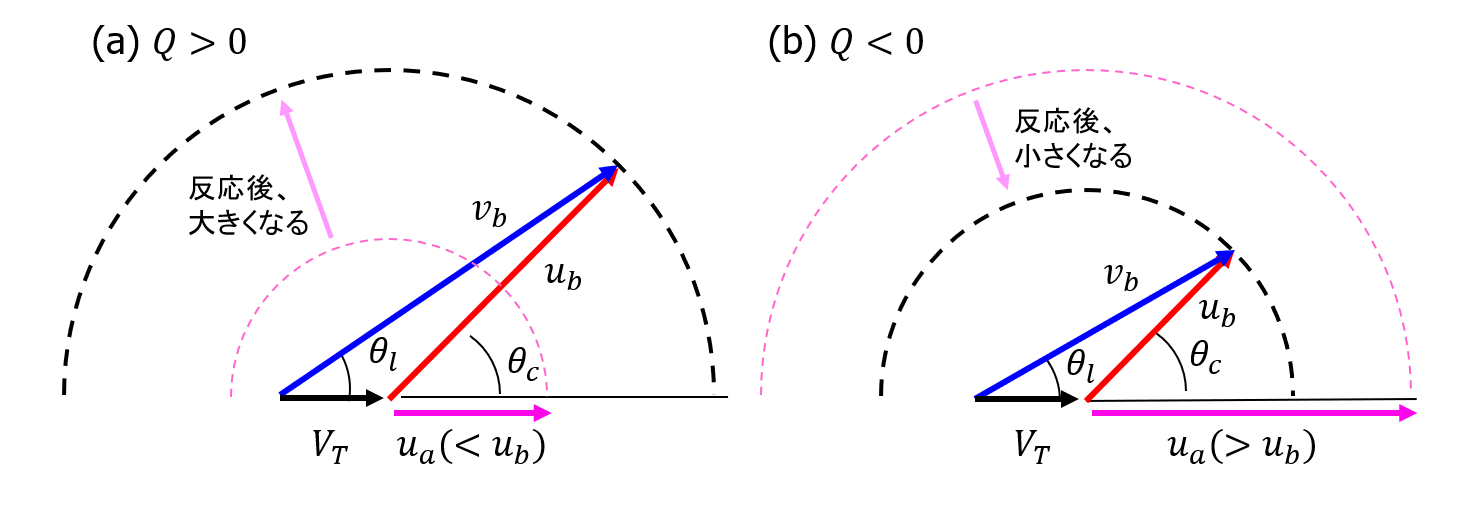
図16 重心系から実験室系への変換。(a) 発熱反応 (b) 吸熱反応
(しきいエネルギー)吸熱反応においては、反応後の運動エネルギーが反応前よりも小さくなるため、ある程度の入射エネルギーが必要である。入射エネルギーがゼロでは反応は起きない。反応を起こすための最低限のエネルギーをしきいエネルギーと呼ぶ。しきいエネルギーを計算するには式(2.48)の平方根の中が正になる条件から求めればよい。すなわち
\begin{align} & \frac{m_X E_{lab}}{m_a+m_X} + Q > 0 \\ & E_{lab} > -\frac{m_a+m_X}{m_X} Q \\ \end{align} となり、しきいエネルギー\(E_{th}\)は次のように定義される。 \begin{align} E_{th} = \left(1+\frac{m_a}{m_X}\right) |Q| \tag{2.49} \\ \end{align}
10. まとめ
以上、原子核反応の概要として、クーロン障壁、原子核反応の表記法、反応のQ値、断面積、運動学について述べた。次章では、原子核反応をさらに理論的に扱うにために必要となる散乱の量子力学について述べる。
注釈
- 概算で用いるには、\(\hbar c \sim 200 \;\mathrm{MeV}\cdot \mathrm{fm}\)でも十分である。
- あくまで例として第1励起準位への非弾性散乱を挙げた。第2励起準位への非弾性散乱であれば、当然ながらQ値は第2励起準位のエネルギーになる。
- あくまで幾何学的サイズであることに注意。実際の断面積は量子力学的効果があり幾何学的サイズとは異なる。
- 例外として単結晶試料の結晶軸に平行に粒子ビームを入射させたときに表面付近原子層に隠れた深い層の原子が反応を起こしづらくなるチャネリングという現象は知られている。
- 低エネルギーで粒子の速度は光速より十分遅いとして非相対論的な運動学を扱う。
参考文献