第4章 共鳴反応 初級編
東京工業大学 片渕竜也
目次
1. はじめに
水で濡らした指でワイングラスの縁をこするときれいな音が出る。音はワイングラスが固有振動数で振動を起こした結果である。指とグラスの間の摩擦で様々な振動数の力が加えられるが、その外力のうち固有振動数のものだけが吸収され、振動の振幅が大きくなった結果、きれいな音が聞こえる。これは、共鳴(もしくは共振、どちらも英語でresonance)と呼ばれる現象の一種である。共鳴現象は、理工学分野の様々な場面で現れ、具体的例は枚挙にいとまがない。原子核反応においても共鳴現象が観測され共鳴反応として知られている。共鳴反応は、低エネルギー中性子の反応を理解する上で非常に重要な概念である。本章では共鳴反応のメカニズム、共鳴公式、共鳴の測定方法などについて解説する。2. 共鳴の発見
1934年、イタリアのFermiのグループは中性子を用いた人工放射能の生成実験を行った文献1。その年のはじめにIrene CurieとFrederic Joliotは人工放射能の生成に成功した。彼らはアルファ線をアルミ箔に当てると放射性のリン(30P)が生成することを発見した。そこでFermiはアルファ線の代わりに中性子を当てればもっとたくさんの放射化が起きるのではないかと考えた注1。中性子は、アルファ粒子と違い原子核のクーロン反発力を受けないので簡単に原子核の中に入っていけるはずである。このFermiの予想は的中した。226Ra-Be中性子源を準備し、片っ端にいろいろな元素に中性子を当ててガイガー計数管で放射能を調べると多くの元素が放射化していることが分かった。結果として40種類以上の元素についての生成放射能データを取得し発表した。これは核データ測定のはしりと言っていい。彼らは実験を行ううちにさらに重要なことに気づいた。試料の周りに水素を含む物質を置くと生成される放射能が大きくなることが分かった。これは中性子が水素と衝突するによりエネルギーを失う「減速」効果の発見である。そして、多くの元素で中性子のエネルギーが低くなると放射化断面積が大きくなることが分かった。
さらにいくつかの元素は完全に減速させるのではなく、中途半端に減速させた場合に放射能が大きくなることが分かった。これはある特定のエネルギー帯で放射化断面積が極大値を持つことを意味する。この実験結果から、BohrそれからBreitとWignerは独立に「共鳴」という概念を提唱した。当時は、まだ原子炉も加速器中性子源もない時代である。素朴な実験の結果からヒントを得て現在まで通用する理論を提唱した理論家の洞察力は敬服に値する。
3. 共鳴と複合核
では、共鳴の具体的な例を見てみよう。例として図1に238Uの中性子全断面積の測定例を示す。横軸は入射中性子エネルギーである。特定の中性子エネルギーの狭いエネルギー範囲で断面積が何桁も大きくなっていることが分かる(縦軸は対数表示であることに注意)。この断面積の鋭いピークが共鳴である。

図1 238Uの共鳴(JENDL-4.0)
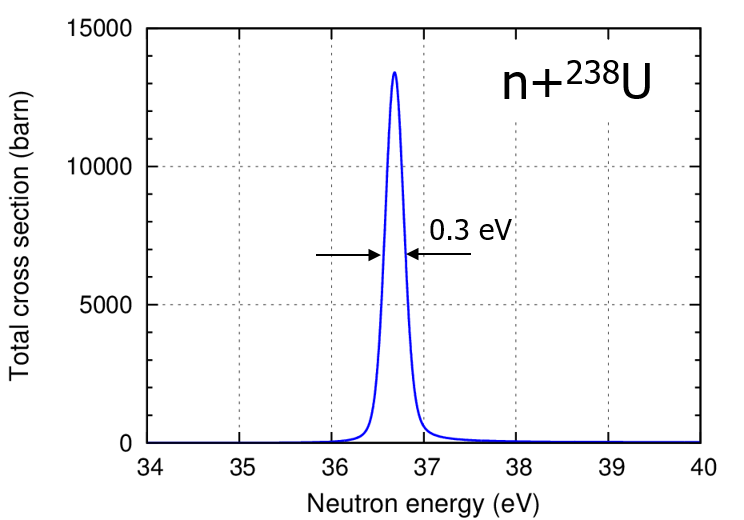
図2 238Uの共鳴
ここで図2の共鳴幅0.3eVを\(\Delta E\)に代入して\(\Delta T\)がどれくらいになるか計算してみよう(ここで\(\hbar c = 197 \:\mathrm{MeV}\cdot\mathrm{fm}\)を用いた)。
\begin{align} \Delta T &= \frac{\hbar}{2 \Delta E} = \frac{\hbar}{2 \times 0.3} =\frac{\hbar c}{0.6 c} = \frac{197 \times 10^6 \times 10^{-15} \: \mathrm{eV} \cdot \mathrm{m}}{0.6 \: \mathrm{eV} \times 3 \times 10^8 \mathrm{m/sec}}\\ &= 1.1 \times 10^{-15} \: \mathrm{sec} \end{align}
\(\Delta T\)として、10-15秒という時間が得られた。これは非常に短い時間のように感じられるが、原子核というミクロなスケールの世界では非常に長い時間である。原子核の世界の典型的な時間スケールとして中性子が原子核を横切る時間が目安になる。
図3 中性子の238U原子核の通過
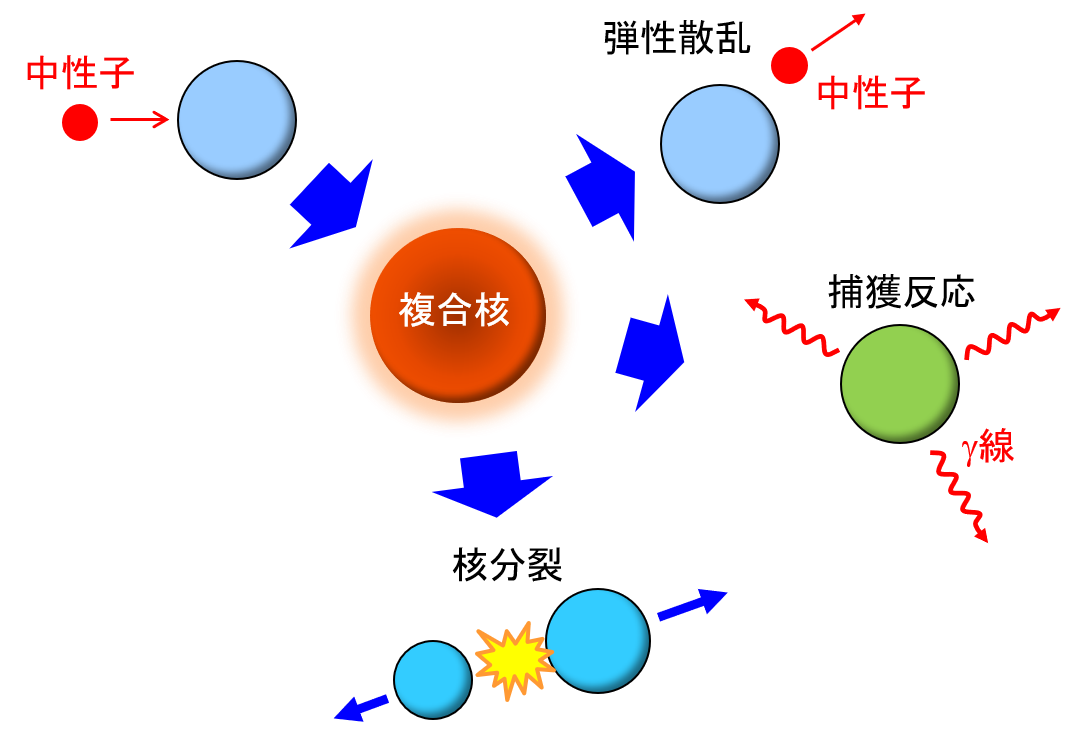
図4 複合核反応と様々な崩壊チャネル
以上のことから、Bohrは複合核模型を提唱した。複合核模型は次の2段階で起きるとする。
- (複合核の形成)入射粒子は標的核と一体となって複合核(compound nucleus)と呼ばれる中間状態を形成する。入射粒子の持ち込んだエネルギーは全ての核子に分配される(熱平衡状態)。
- (複合核の崩壊)複合核は最終生成物に崩壊する。複合核の寿命は長いのでどのように形成されたのか複合核は覚えていない。そのため崩壊の仕方(崩壊率)は形成過程に依存しない。
4. 共鳴と量子力学
 図5 核内波動関数が分からなくても核表面の対数
図5 核内波動関数が分からなくても核表面の対数微分が与えられれば核外波動関数は決まる。
第3章で述べたように散乱断面積を求めるには原子核の内側と外側の波動関数を考え、ポテンシャル表面での波動関数の接続条件から位相のずれを計算し断面積を求める。しかし、実際には正確な内部波動関数を求めることは困難である。なぜなら、原子核中の核子の波動関数の導出は、単純な一体ポテンシャル中の一粒子の波動関数を求めるようなものではなく、複雑な多体問題となり簡単には求められないからである。そこで原子核の内部波動関数の詳細を知らなくても議論できる道具立てが必要になる。内部波動関数\(\phi_{in}(r)\)と外部波動関数\(\phi_{out}(r)\)は原子核のポテンシャル表面で連続的に接続しなくてはならない。つまり、原子核表面(\(r=R\))で \begin{align} \phi_{in}(R) &= \phi_{out}(R) \tag{4.2} \end{align} である。また、同様に波動関数の微分係数も連続に接続しなくてはならない。つまり、
\begin{align} \left. \frac{d \phi_{in}}{dr}\right|_{r=R} &= \left. \frac{d \phi_{out}}{dr}\right|_{r=R} \tag{4.3} \end{align} である。対数微分を用いると次のようにまとめて書くことができる。
\begin{align} \left. \frac{1}{\phi_{in}}\frac{d \phi_{in}}{dr}\right|_{r=R} = \left. \frac{1}{\phi_{out}}\frac{d \phi_{out}}{dr}\right|_{r=R} \tag{4.4} \end{align} この接続条件が波動関数の拘束条件となるわけであるが、逆に言うと対数微分さえ与えられれば外部波動関数が決まり(図5)、外部波動関数が決まれば断面積も求まる。つまり、外部波動関数から見れば内部波動関数の情報は原子核表面の対数微分に集約されていると言っていい。したがって、対数微分を用いると内部波動関数の詳細に触れることなく議論を展開することが可能になる。
以下、簡単のために軌道角運動量がゼロ(\(l=0\))の中性子が起こす共鳴について議論する。第3章に示したように\(l=0\) の外部波動関数は散乱係数\(S\)を用いて次のように書ける。
\begin{align} \phi_{out}(r) &= \frac{1}{2ikr}(S e^{ikr} - e^{-ikr}) \tag{4.5} \end{align} \(1/r\)の因子を除いた方が取り扱いが簡単になるので次のように定義した\(u(r)\)を以下の議論に用いる。
\begin{align} u(r) = r \phi_{out}(r) &= \frac{1}{2ik}(S e^{ikr} - e^{-ikr}) \tag{4.6} \end{align} \(u(r)\)のポテンシャル表面(\(r = R\))での対数微分として\(F\)を定義する(このあとの表式を慣例に合わせるためにマイナスを掛けて符号を逆にしている)。
\begin{align} F &= - \left. \frac{1}{u}\frac{d u}{dr}\right|_{r=R} = \frac{ikSe^{ikR}+ike^{-ikR}}{Se^{ikR}-e^{-ikR}} = ik\frac{Se^{ikR}+e^{-ikR}}{Se^{ikR}-e^{-ikR}} \tag{4.7} \end{align} これを\(S\)について書き直すと
\begin{align} S = \frac{F - ik}{F + ik} e^{-2ikR} \tag{4.8} \end{align} となる。これで対数微分\(F\)で散乱係数\(S\)を表すことができた。これを式(3.91)と(3.94)に代入してやれば散乱断面積\(\sigma_s\)と反応断面積\(\sigma_r\)が求まる。すなわち
\begin{align} \sigma_s &= \frac{\pi}{k^2} |1-S|^2 = \frac{\pi}{k^2} \left|1-\frac{F - ik}{F + ik} e^{-2ikR}\right|^2 \tag{4.9}\\ \sigma_r &= \frac{\pi}{k^2} (1-|S|^2) = \frac{\pi}{k^2} \left(1-\left|\frac{F - ik}{F + ik}\right|^2\right) \tag{4.10}\\ \end{align} である。この式からさらに断面積の具体的な形を求めてみよう。以下、\(|S|=1\)の場合と\(|S|\neq1\)の場合に分けて議論を進める。
(\(|S|=1\)の場合) まずは、\(|S|=1\)すなわち弾性散乱しか起きない場合を考えよう。式(4.9)を変形すると注2
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{F + ik} \right|^2 \tag{4.11} \end{align} という形にできる。これで\(F\)を含まない第1項と\(F\)を含む第2項に分けることができた。
それぞれの項の物理的意味について見ていこう。まず、第1項を無視して第2項のみで断面積を考えてみよう。つまり、
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|\frac{k}{F + ik} \right|^2 \tag{4.12} \end{align} とする。対数微分\(F\)は、当然、中性子エネルギー\(E\)に対する関数である。式(4.12)から分かるように\(F\)が0になるとき、\(\sigma_s\)は最大になる。そこで\(E = E_r\)の時、\(F\)が0になるとする。すなわち \begin{align} F(E_r) = 0 \tag{4.13} \end{align} である。\(E = E_r\)近傍で\(F\)を表すと \begin{align} F(E) &= 0 + \left. \frac{dF}{dE}\right|_{E_r} (E-E_r) + \:... \tag{4.14}\\ \end{align} である。ここで\(\Gamma_{sc}\)を
\begin{align} \left. \frac{dF}{dE}\right|_{E_R} = \frac{2k}{\Gamma_{sc}} \tag{4.15} \end{align} と定義すると\(F\)は
\begin{align} F \sim \frac{2k}{\Gamma_{sc}} (E-E_r) \tag{4.16} \end{align} となり、これを式(4.12)に代入すると\(\sigma_s\)は
\begin{align} \sigma_s &\sim \frac{4\pi}{k^2} \frac{k^2}{(\frac{2}{\Gamma_{sc}})^2 k^2 (E-E_r)^2 + k^2} \\ &= \frac{\pi}{k^2} \frac{\Gamma_{sc}^2}{ (E-E_r)^2 + (\Gamma_{sc}/2)^2} \tag{4.17} \end{align} となる。式(4.17)は、Breit-Wignerの一準位公式と呼ばれ、1本の共鳴による中性子の弾性散乱断面積のエネルギー依存性を表す式である。
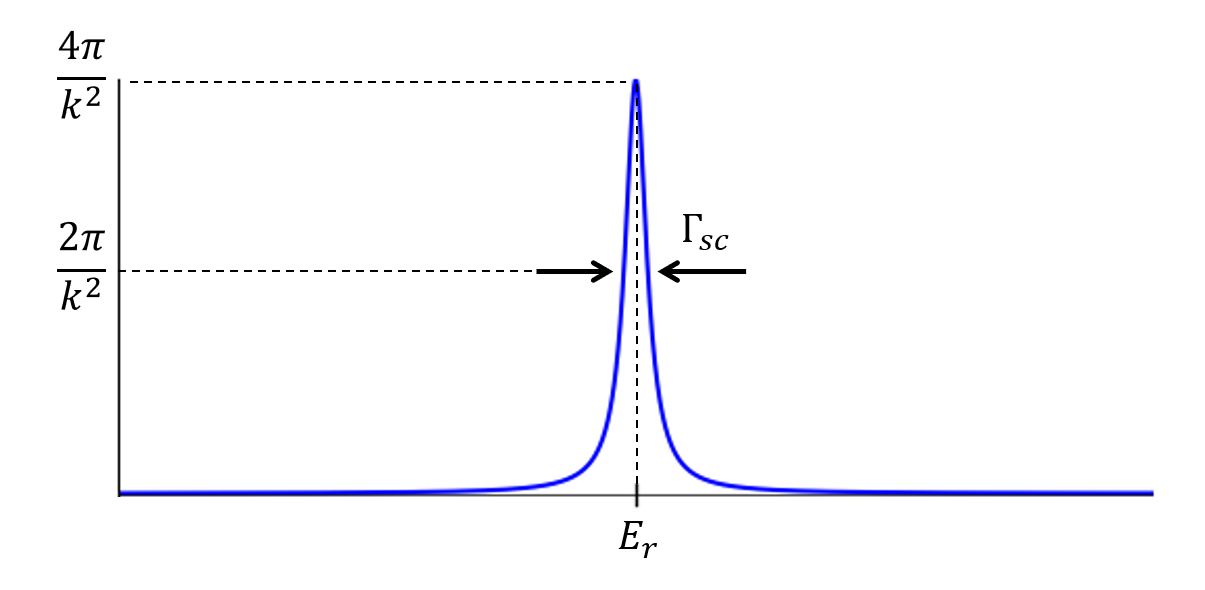
図6 共鳴ピークとBreit-Wignerの一準位公式
\(E_r\)は共鳴エネルギーである。\(\sigma_{s}\)は\(E=E_r\)のとき最大となる。代入すると最大値は \begin{align} \sigma_{s} = \frac{\pi}{k^2}\frac{\Gamma_{sc}^2}{(E_r-E_r)^2+\Gamma_{sc}^2/4} = \frac{\pi}{k^2}\frac{\Gamma_{sc}^2}{\frac{\Gamma_{sc}^2}{4}} = \frac{4 \pi}{k^2} \end{align} となる。
\(\Gamma_{sc}\)は共鳴幅と呼ばれる。\(E=E_r + \frac{\Gamma_{sc}}{2}\)もしくは\(E=E_r - \frac{\Gamma_{sc}}{2}\)を代入すると \begin{align} \sigma_{s} = \frac{\pi}{k^2}\frac{\Gamma_{sc}^2}{(\frac{\Gamma_{sc}}{2})^2+\Gamma_{sc}^2/4} = \frac{\pi}{k^2}\frac{\Gamma_{sc}^2}{\Gamma_{sc}^2/4+\Gamma_{sc}^2/4} = \frac{2 \pi}{k^2} \end{align}
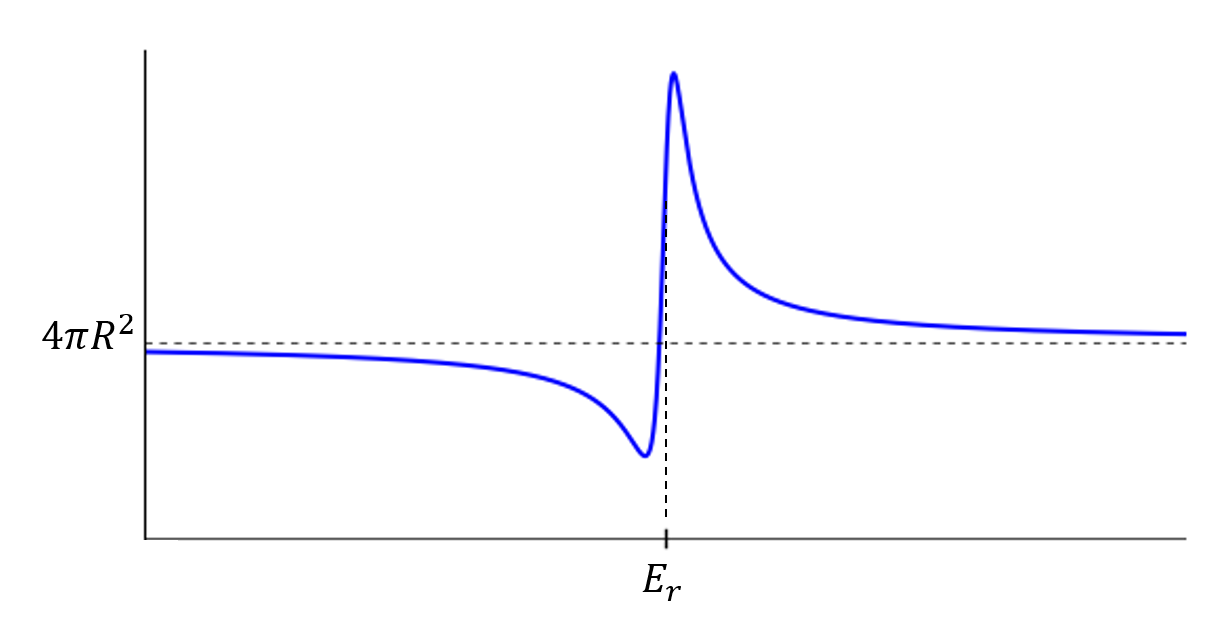
図7 共鳴近傍の散乱断面積(\(l=0\))
実際には、式(4.11)にあるように第1項が絶対値の中に含まれている。第1項は共鳴ではなくポテンシャル散乱によるものである。つまり、ポテンシャル散乱と共鳴散乱の間で干渉が生じる。式(4.11)の\(F\)に式(4.16)を代入すると
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{F + ik} \right|^2 \\ &\sim \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{\frac{2k}{\Gamma_{sc}} (E-E_r) + ik} \right|^2 \\ &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{\Gamma_{sc}/2}{E-E_r + i\Gamma_{sc}/2} \right|^2 \tag{4.18}\\ \end{align} となる。\(E\)が共鳴点\(E_r\)より小さいと第2項は共鳴点より小さくなりポテンシャル散乱との干渉が弱め合いとなる。逆に\(E\)が\(E_r\)より大きくなると強め合いとなる。したがって、断面積のエネルギー依存性は図7のような形になる。
共鳴点から十分離れると第2項は小さくなり無視できるので断面積には第1項のみが寄与する。つまり、
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR \right|^2 = \frac{4\pi}{k^2} \sin^2 kR \tag{4.19}\\ \end{align} となる。十分な低エネルギーの場合(\(kR \ll 1\))には、
\begin{align} \sigma_s \sim \frac{4\pi}{k^2} (kR)^2 = 4\pi R^2 \tag{4.20}\\ \end{align} これはまさに第3章で扱った剛体球による散乱と同じ結果が得られた。つまり、低エネルギー中性子の散乱断面積は、原子核表面での剛体球散乱と原子核内部の共鳴散乱の干渉で記述できることが分かった。
(\(|S|<1\)の場合) 次に\(|S|\)が1より小さい場合、つまり反応も起こる場合について考えよう。\(|S|=1\)のときと同様に\(F=0\)になるエネルギー近傍で断面積を求めるが、\(|S|<1\)の場合には\(F\)が複素数になることに気をつける必要がある注3。そこで、エネルギーが\(E_0 = \epsilon_0 + i \frac{\Gamma_r}{2}\)のときに\(F\)がゼロにになるとする。すなわち \begin{align} &E_0 = \epsilon_0 + i \frac{\Gamma_r}{2} \tag{4.17}\\ &F(E_0) = 0 \end{align} である。\(F\)を\(E_0\)の周りで展開すると
\begin{align} F(E)= 0 + \left. \frac{dF}{dE}\right|_{E_0}(E-E_0) + \:... \tag{4.18}\\ \end{align} となる。ここで\(F\)は複素数なので、そのエネルギー微分も複素数である。そこで実部、虚部を次のように書くと
\begin{align} \mathrm{Re}\left(\left. \frac{dF}{dE}\right|_{E_0} \right) &= \frac{2k}{\Gamma_{sc}} \tag{4.19}\\ \mathrm{Im}\left(\left. \frac{dF}{dE}\right|_{E_0} \right) &= k \alpha \tag{4.20}\\ \left. \frac{dF}{dE}\right|_{E_0} &= \frac{2k}{\Gamma_{sc}} + i k \alpha \tag{4.21} \end{align} 微分係数は
\begin{align} \left. \frac{dF}{dE}\right|_{E_0} &= \frac{2k}{\Gamma_{sc}} + i k \alpha \tag{4.22} \end{align} となる。式(4.18)に代入すると\(F\)は\(E_0\)近傍で
\begin{align} F &\sim \left(\frac{2k}{\Gamma_{sc}} + i k \alpha\right) \left(E-\epsilon_0 - i \frac{\Gamma_r}{2}\right) \\ &= \frac{2k}{\Gamma_{sc}}\left(E-\epsilon_0 - \frac{\alpha \Gamma_{sc} \Gamma_r}{4}\right) + ik \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) \\ &= \frac{2k}{\Gamma_{sc}}(E- E_r) + ik \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) \tag{4.23} \end{align} となる。ここで\(E_r\)を
\begin{align} E_r = \epsilon_0 + \frac{\alpha \Gamma_{sc} \Gamma_r}{4} \tag{4.24} \end{align} とした。式(4.23)を用いて\(\sigma_r\)と\(\sigma_s\)を求めよう。まず、\(\sigma_r\)を求める。式(4.10)を変形すると注4
\begin{align} \sigma_r &= \frac{\pi}{k^2} \left(1-\left|\frac{F - ik}{F + ik}\right|^2\right) \\ &= \frac{\pi}{k^2} \frac{4 k \mathrm{Im}(F)}{|F|^2 +2 k \mathrm{Im}(F) + k^2} \tag{4.25}\\ \end{align} となる。\(F\)に式(4.23)を代入するとと注5
\begin{align} \sigma_r &\sim \frac{\pi}{k^2} \frac{4 k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)}{\left(\frac{2k}{\Gamma_{sc}}\right)^2(E- E_r)^2 +k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)^2 +2 k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) + k^2}\\ &= \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma_r}{(E- E_r)^2 + \left(\frac{\Gamma_r + \Gamma_{sc}}{2}\right)^2} \tag{4.26}\\ \end{align} となる。これが反応に関するBreit-Wignerの一準位公式である。断面積のエネルギー依存性は図と同様の形となり、共鳴の幅は\(\Gamma_r + \Gamma_{sc}\)である。\(\Gamma_r + \Gamma_{sc}\)はしばしば \(\Gamma=\Gamma_r + \Gamma_{sc}\)と表され、\(\Gamma\)は全幅と呼ばれる。\(\Gamma_{sc}, \Gamma_r\)は部分幅と呼ばれる。
散乱断面積についても式(4.9)に式(4.23)を代入すると注6
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{F + ik} \right|^2 \\ &\sim \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{\frac{\Gamma_{sc}}{2}}{(E- E_r) + i\left(\frac{\Gamma}{2}\right)} \right|^2 \tag{4.27}\\ \end{align} が得られる。式(4.18)と同様にポテンシャル散乱と共鳴散乱の干渉となっている。第2項のみの場合には断面積は以下に示すように式(4.17)と同様の形になる。 \begin{align} \sigma_s &= \frac{\pi}{k^2} \frac{\Gamma_{sc}^2}{ (E-E_r)^2 + \left(\frac{\Gamma}{2}\right)^2} \tag{4.28}\\ \end{align} ここでBreit-Wignerの一準位公式を以下にまとめておく。
\begin{align}
&\sigma_s = \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{\frac{\Gamma_{sc}}{2}}{(E- E_r) + i\left(\frac{\Gamma}{2}\right)} \right|^2 \tag{4.29}\\
&\sigma_r = \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma_r}{(E- E_r)^2 + \left(\frac{\Gamma}{2}\right)^2} \tag{4.30}\\
&ここで \:\Gamma=\Gamma_r + \Gamma_{sc}
\end{align}
(部分幅\(\Gamma_r\)の意味)ここで\(\Gamma_r\)の物理的意味についてもう少し考えてみよう。
そもそも\(\Gamma_r\)は、\(F\)が0になるエネルギーの虚部として導入された。すなわち
\begin{align} &E_0 = \epsilon_0 + i \frac{\Gamma_r}{2} \tag{4.31}\\ &F(E_0) = 0 \tag{4.32} \end{align} である。対数微分が0になるときに共鳴散乱の振幅が大きくなる、すなわちそのエネルギーで系が共鳴状態になることを意味する。しかし、エネルギーが虚数部を持つとはどういうことなのだろうか。
時間に依存するシュレーディンガー方程式からエネルギー固有値\(E\)を持つ系の波動関数\(\phi(r,t)\)は、時間と空間で変数分離ができて \begin{align} \phi(r,t) &= \exp\left(i\frac{E}{\hbar}t\right)u(r) \tag{4.33}\\ \end{align} と書ける。
エネルギーが実数であれば、粒子の確率分布を計算すると \begin{align} |\phi|^2 &= |u(r)|^2 \tag{4.34} \end{align} となり、時間依存因子は消える。つまり当然のことながら時間とともに変化しない。
一方、エネルギーとして式(4.31)で与えられる複素数を代入してやると
\begin{align} \phi(r,t) &= \exp\left(i\frac{\epsilon_0 + i\frac{\Gamma_r}{2}}{\hbar}t\right)u(r) \\ &= \exp\left(i\frac{\epsilon_0}{\hbar}t\right)\exp\left(-\frac{\Gamma_r}{2\hbar}t\right)u(r) \tag{4.35}\\ \end{align} となり、絶対値の2乗をとり粒子の確率分を求めると \begin{align} |\phi|^2 &= \exp\left(-\frac{\Gamma_r}{\hbar}t\right)|u(r)|^2 \tag{4.36} \end{align} となる。このことから、\(\hbar/\Gamma_r\)の寿命で粒子数が減少することが分かる。
しかし、粒子数が減少するとはどういうことなのだろうか。それには元の波動関数が何を扱っているのかを考えてみると分かる。出発点となっている方程式は中性子と標的原子核の波動関数についてのものである。反応を起こすと系は異なる粒子の組み合わせ(チャンネル)に変わる、すなわち弾性散乱チャンネルから消える。したがって、式(4.36)は共鳴を起こした複合核状態から弾性散乱以外のチャンネルに遷移して消えていくことを意味している。つまり、\(\Gamma_r\)は複合核から反応チャンネルへの遷移強度を表しているのである。
5. 複合核模型と共鳴公式
上で求めたBreit-Wignerの一準位公式の中に複合核模型の仮定がどのように現れているのか見てみよう。まず、式(4.30)を一般の場合に拡張する。弾性散乱以外に反応\(a, b, c ...\)といろいろな反応が起きるとする。このとき全幅\(\Gamma\)は、起きうる全ての反応の部分幅を足したものとなる。つまり、
\begin{align} \Gamma = \Gamma_{sc} + \Gamma_a + \Gamma_b + \Gamma_c ... \tag{4.37} \end{align} である。ここで\(\Gamma_{sc}\)は弾性散乱の部分幅、\(\Gamma_a, \Gamma_b, \Gamma_c ...\)は、反応\(a, b, c ...\)の部分幅である。
このとき、反応\(a\)についての共鳴公式は
\begin{align} &\sigma_a = \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma_a}{(E- E_r)^2 + \left(\frac{\Gamma}{2}\right)^2} \tag{4.38}\\ \end{align} となる。
式(4.38)を変形すると
\begin{align} &\sigma_a = \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma}{(E- E_r)^2 + \left(\frac{\Gamma}{2}\right)^2} \times \frac{\Gamma_a}{\Gamma} \tag{4.39}\\ \end{align} となる。
既に述べたように複合核模型は次の2段階で原子核反応が起こると仮定している。
- (複合核の形成)入射粒子は標的核と一緒になって複合核という準安定な中間状態をつくる。
- (複合核の崩壊)複合核は最終的な生成物へ崩壊する。
\begin{align} (反応aの断面積) = (複合核形成断面積) \times (チャンネルaへの複合核崩壊確率) \tag{4.40} \end{align} となる。
実際、式(4.39)はこの形になっている。部分幅は、上記で述べたように複合核から各反応チャンネルへの遷移強度を表す。式中の
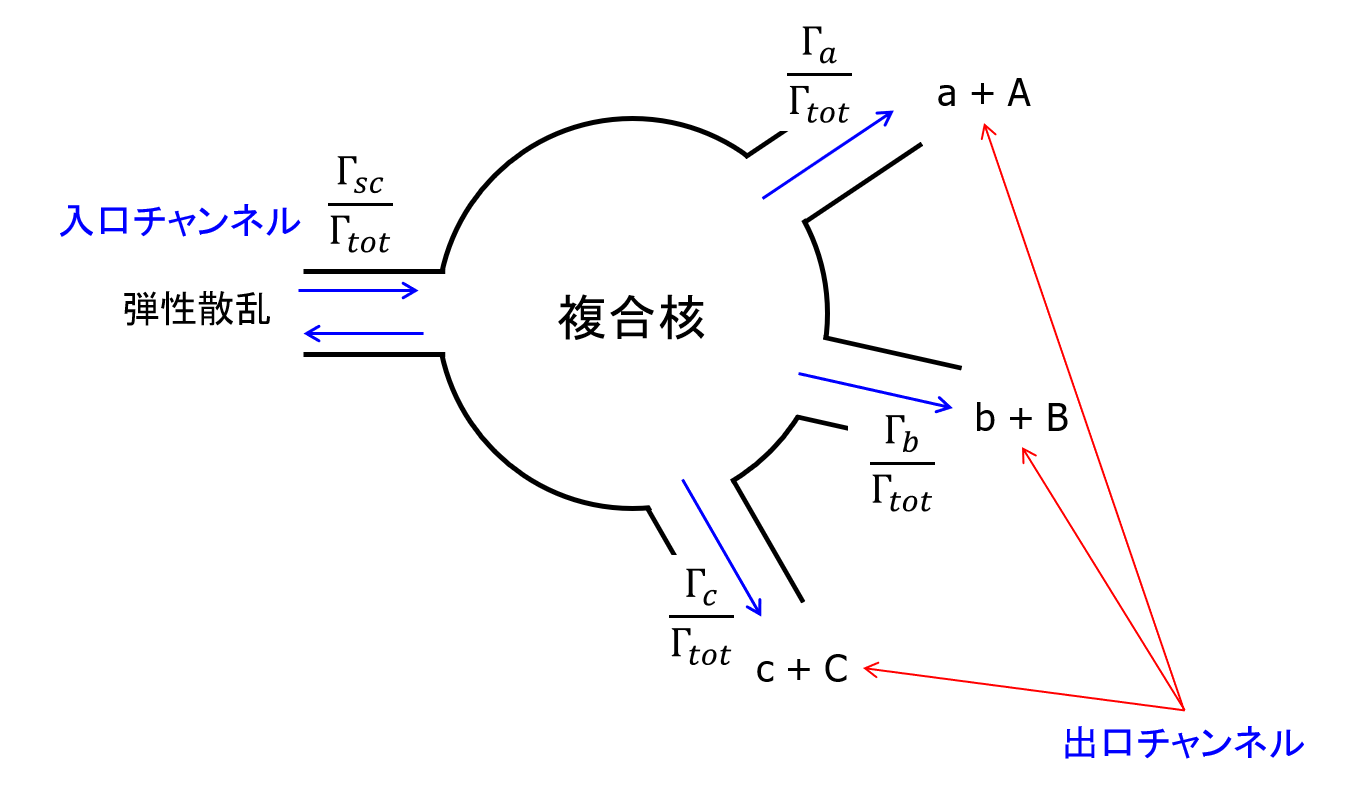
図8 複合核と反応チャンネルの模式図
一方、式(4.39)の残りの部分は複合核形成断面積である。つまり、複合核形成断面積を\(\sigma_c\)とすれば、
\begin{align} \sigma_c = \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma}{(E- E_r)^2 + \left(\frac{\Gamma}{2}\right)^2} \tag{4.42} \end{align} である。\(E = E_r\)のときに
\begin{align} \sigma_c(E_r) = \frac{4\pi}{k^2} \frac{\Gamma_{sc}}{\Gamma} \tag{4.43} \end{align} となり、式(4.41)と同様の全幅に対する部分幅の比\(\Gamma_{sc}/\Gamma\)を含むことが分かる。これは時間反転の対称性から時間を逆回しにしてやると複合核の崩壊は、複合核の形成に逆転するためである。反応\(a\)の系 \(a + A\)から複合核を形成する断面積を\(\sigma_{c\leftarrow a}\)とすると部分幅\(\Gamma_a\)に比例する。つまり、
\begin{align} \sigma_{c\leftarrow a} \propto \Gamma_a \tag{4.44} \end{align} である。そのため式(4.43)の形成断面積に入口チャンネルでもある弾性散乱チャンネルの部分幅が含まれている。図に複合核の形成と各チャンネルへの崩壊を模式的に図示したものを示す。
6. 中性子核データと共鳴
中性子核データでは、弾性散乱、中性子捕獲反応、核分裂反応が特に重要である。それらに対する部分幅を\(\Gamma_n, \Gamma_\gamma, \Gamma_f\)で表す。これらをBreit-Wignerの式に代入すると弾性散乱断面積\(\sigma_n\)、捕獲断面積\(\sigma_\gamma\)、核分裂断面積\(\sigma_f\)はそれぞれ以下のようになる(ただし、\(l=0\)の場合であることに注意)。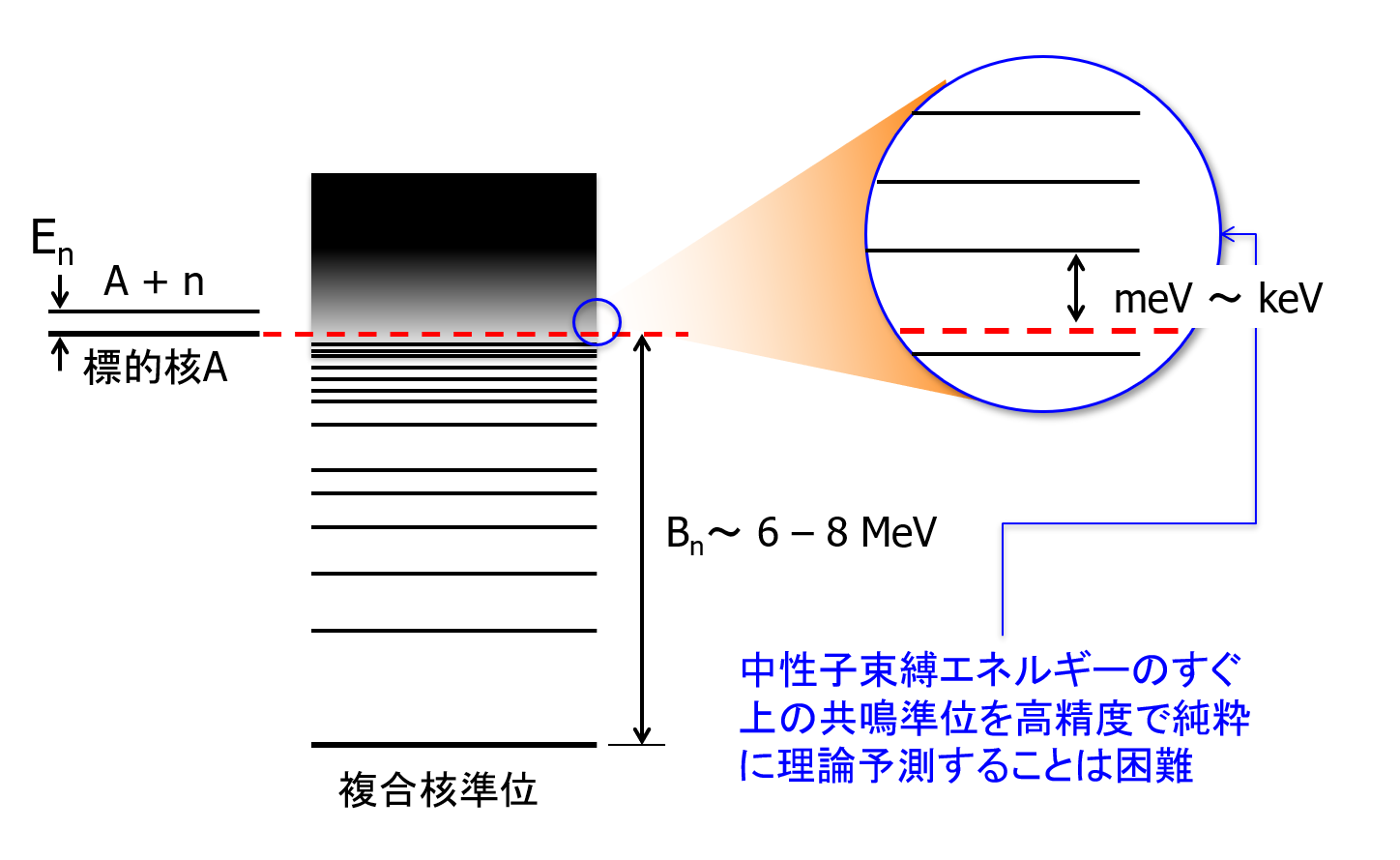
図9 複合核と反応チャンネルの模式図
ここで注意すべきは、Breit-Wignerの一準位公式は、共鳴断面積のエネルギー依存性を共鳴パラメータにより表現するための公式に過ぎず、共鳴を予言するものではないことである。現在の原子核物理では個々の共鳴のエネルギーや幅を純粋理論的に求めることは不可能である。中重核の中性子束縛エネルギーは、7 MeV程度なので標的核が低エネルギー中性子を吸収して複合核になると、その励起エネルギーは7 MeV程度になる。中性子束縛エネルギーよりも高い励起エネルギーに複合核の準安定状態が存在すると共鳴反応が起きる。共鳴を起こす準位は中性子束縛エネルギーの上、meV\(\sim\)keVの領域に存在している。このことは、理論計算で共鳴準位を予測するには、MeVオーダーの励起エネルギーの準位をmeVの精度で求める必要があり、そのような精度での計算は事実上不可能である。また、求めるべきものも単純な一体ポテンシャル中の一粒子準位ではなく、複雑な多体問題となるため解くのは困難である。
したがって、現在のところ、共鳴パラメータは実験により測定する以外に方法はない。核データライブラリに格納されている共鳴パラメータは、測定により観測した共鳴ピークに対し共鳴公式を適用し決定したものである。次の節で共鳴の測定について解説する。
7. 共鳴の測定
共鳴を観測するには断面積を中性子エネルギーの関数として高分解で測定する必要がある。それには通常、飛行時間法が用いられる。飛行時間法は、中性子源から試料までの距離を中性子が飛行する時間を計測し、飛行時間から中性子のエネルギーを算出する方法である。

図10 中性子飛行時間法
図9にあるように飛行距離を\(L\)、飛行時間を\(T\)としたとき、中性子の速さ\(v\)は \begin{align} v = \frac{L}{T} \tag{4.48} \end{align} となる。したがって、中性子の運動エネルギー\(E_n\)は \begin{align} E_n = \frac{1}{2}m_n v^2 = \frac{m_n}{2}\left(\frac{L}{T}\right)^2 \tag{4.49} \end{align} となる。ここで\(m_n\)は中性子の質量である。中性子の静止質量939.565 MeVを代入すると \begin{align} E_n = \frac{m_n}{2}\left(\frac{L}{T}\right)^2 = \frac{m_n c^2}{2 c^2}\left(\frac{L}{T}\right)^2 = \frac{939.565}{2\times0.2997^2}\left(\frac{L}{T}\right)^2 = 5230 \times \left(\frac{L}{T}\right)^2 \tag{4.50} \end{align} となる。ここで\(c\)は光速であり、値0.2997 m/nsを代入した。上式を整理して実用的に使いやすい公式として以下にまとめる。 \begin{align} E_n &= \left(\frac{72.3 \times L}{T}\right)^2 \tag{4.51}\\ &E_n : \text{中性子エネルギー (MeV または eV)}\\ &L : \text{飛行距離 (m)}\\ &T : \text{飛行時間 (ns または}\mu\rm{s}) \end{align} 単位は飛行時間がnsであれば、中性子エネルギーはMeV、\(\mu\)sであればeVとして与えられる。一方、飛行時間\(T\)について書き直すと \begin{align} T &= \frac{72.3 \times L}{\sqrt{E_n}} \tag{4.52}\\ \end{align} である。
図11 捕獲反応測定の実験セットアップ
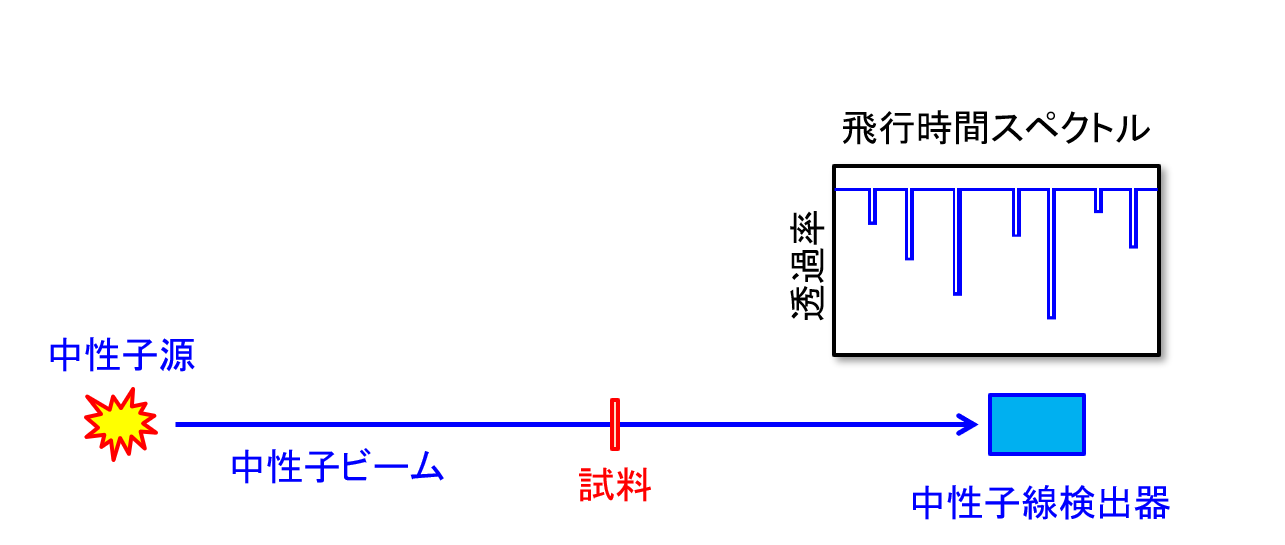
図12 透過測定の実験セットアップ
飛行時間法を用いた断面積測定は大きく分けて二通りある。ひとつは、試料で起きる中性子核反応からの放出粒子を直接測定する方法である。例えば、中性子捕獲反応であれば、試料からの中性子捕獲ガンマ線をガンマ線検出器で検出する。核分裂反応であればを試料で起きる核分裂反応からの核分裂片を核分裂計数管などで検出する。図11に例として捕獲ガンマ線を計測する場合の実験セットアップを示す。検出した事象を飛行時間についてヒストグラムとすることで飛行時間スペクトルが得られる。断面積の共鳴構造は飛行時間スペクトルに反映される。共鳴エネルギーに相当する飛行時間で検出器の係数が鋭く上昇する。飛行時間は式(4.51)を用いてエネルギーに変換できる。
もう一つは試料を透過してくる中性子を検出する方法である。この方法では試料を透過してきた中性子の数を計測する。図12に透過測定の実験セットアップを示す。試料中で中性子が散乱や反応を起こすと直進する中性子の数が減る。したがって、共鳴が存在する飛行時間で中性子の数が鋭く減少する。つまり、反応を直接計測する場合の飛行時間スペクトルを逆さまにしたような結果が得られる。中性子の透過率を\(T_r\)とすると全断面積\(\sigma_t\)、試料原子密度\(N\)、試料厚さ\(t\)を用いて次のように書ける。
\begin{align} T_r = e^{-N\sigma t} \tag{4.52}\\ \end{align} 測定で得られた飛行時間スペクトルに対し共鳴公式を当てはめ共鳴パラメータが決定される。共鳴解析コードとしてSAMMYやREFITといったコードが広く使われている。共鳴解析の例を図13に示す。

図13 241Amの中性子捕獲断面積の測定値(黒点)と共鳴解析の結果(赤線)(日本原子力研究開発機構 Gerard Rovira氏提供)
注釈
-
チャドウィックによって中性子が発見されたのが、1932年である。チャドウィックによる中性子発見後、フェルミがかなり早い段階でこの実験を考えていたことが分かる。中性子はジョリオとキュリーが最初に観測していたが、ガンマ線と誤認したため発見者としての栄誉を逃した。チャドウィックがより洗練された実験を行い、中性子という新たな粒子の発見者となった。中性子の発見者としてノーベル賞をもらえなかったジョリオとキュリーは、その後、最初の人工放射能の生成を行い晴れてノーベル賞を受賞する。この後、ジョリオとキュリーの実験に触発されたフェルミが中性子を用いて放射能の生成実験を行い、さらにフェルミの実験に触発されたハーン等がウランに中性子を当てて核分裂を発見するという、当時の原子核物理がいかにお互い影響し合いながら急速に進んでいたかが分かる。
-
式変形を以下に示す。
\begin{align} \sigma_s &= \frac{\pi}{k^2} \left|1-\frac{F - ik}{F + ik} e^{-2ikR}\right|^2 = \frac{\pi}{k^2} \left|e^{2ikR} -\frac{F - ik}{F + ik} \right|^2 \\ &= \frac{\pi}{k^2} \left|e^{2ikR} -\frac{F + ik - 2ik}{F + ik} \right|^2 = \frac{\pi}{k^2} \left|e^{2ikR} -1 + \frac{2ik}{F + ik} \right|^2 \\ &= \frac{\pi}{k^2} \left|e^{ikR}(e^{ikR} -e^{-ikR}) + \frac{2ik}{F + ik} \right|^2 = \frac{\pi}{k^2} \left|2i e^{ikR}\sin kR + \frac{2ik}{F + ik} \right|^2 \\ &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{F + ik} \right|^2 \end{align} -
-
式変形を以下に示す。
\begin{align} \sigma_r &= \frac{\pi}{k^2} \left(1-\left|\frac{F - ik}{F + ik}\right|^2\right) \\ &= \frac{\pi}{k^2} \left(1-\left|\frac{\mathrm{Re}(F) + i\mathrm{Im}(F) - ik}{\mathrm{Re}(F) + i\mathrm{Im}(F) + ik}\right|^2\right) \\ &= \frac{\pi}{k^2} \left(1-\frac{\mathrm{Re}(F)^2 + (\mathrm{Im}(F) - k)^2}{\mathrm{Re}(F)^2 + (\mathrm{Im}(F) + k)^2}\right) \\ &= \frac{\pi}{k^2} \left(1-\frac{\mathrm{Re}(F)^2 + \mathrm{Im}(F)^2 -2 k \mathrm{Im}(F) + k^2}{\mathrm{Re}(F)^2 + \mathrm{Im}(F)^2 +2 k \mathrm{Im}(F) + k^2}\right) \\ &= \frac{\pi}{k^2} \left(1-\frac{|F|^2 -2 k \mathrm{Im}(F) + k^2}{|F|^2 +2 k \mathrm{Im}(F) + k^2}\right) \\ &= \frac{\pi}{k^2} \left(1-1 + \frac{4 k \mathrm{Im}(F)}{|F|^2 +2 k \mathrm{Im}(F) + k^2}\right) \\ &= \frac{\pi}{k^2} \frac{4 k \mathrm{Im}(F)}{|F|^2 +2 k \mathrm{Im}(F) + k^2}\\ \end{align} -
式変形を以下に示す。
\begin{align} \sigma_r &= \frac{\pi}{k^2} \frac{4 k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)}{\left(\frac{2k}{\Gamma_{sc}}\right)^2(E- E_r)^2 +k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)^2 +2 k^2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) + k^2}\\ &= \frac{\pi}{k^2} \frac{4 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)}{\left(\frac{2}{\Gamma_{sc}}\right)^2(E- E_r)^2 + \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)^2 +2 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) + 1}\\ &= \frac{\pi}{k^2} \frac{4 \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right)}{\left(\frac{2}{\Gamma_{sc}}\right)^2(E- E_r)^2 +\left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0 )+1\right)^2}\\ &= \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma_r +\alpha\Gamma_{sc}^2(E-\epsilon_0)}{(E- E_r)^2 + \left(\frac{\Gamma_r + \Gamma_{sc} + \alpha\Gamma_{sc}(E-\epsilon_0 )}{2}\right)^2}\\ \end{align} \begin{align} \sigma_r &= \frac{\pi}{k^2} \frac{\Gamma_{sc}\Gamma_r}{(E- E_r)^2 + \left(\frac{\Gamma_r + \Gamma_{sc}}{2}\right)^2}\\ \end{align} -
式変形を以下に示す。
\begin{align} \sigma_s &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{F + ik} \right|^2 \\ &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{k}{\frac{2k}{\Gamma_{sc}}(E- E_r) + ik \left(\frac{\Gamma_r}{\Gamma_{sc}}+\alpha(E-\epsilon_0)\right) + ik} \right|^2 \\ &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{\frac{\Gamma_{sc}}{2}}{(E- E_r) + i\left(\frac{\Gamma_{sc} + \Gamma_r+\alpha\Gamma_{sc}(E-\epsilon_0)}{2}\right)} \right|^2 \\ &= \frac{4\pi}{k^2} \left|e^{ikR}\sin kR + \frac{\frac{\Gamma_{sc}}{2}}{(E- E_r) + i\left(\frac{\Gamma_{sc} + \Gamma_r}{2}\right)} \right|^2 \\ \end{align}
参考文献
- D. W. Miller et al., Physical Review 88, 83 (1952).
- H. H. Barschall, Physical Review 86, 431 (1952).
- H. Feshbach and V. F. Weisskopf, Physical Review 76, 1550 (1949).
- H. Feshbach, C. E. Porter and V. F. Weisskopf, Physical Review 96, 448 (1954).
- R. L. Varner et al., Physics Reports 201, 57 (1991).
- A. J. Koning and J. P. Delaroche, Nuclear Physics A 713, 231 (2003).
- S. Kunieda et al, Journal of Nuclear Science and Technology 44, 838 (2007).