第3章 散乱の理論 初級編
東京工業大学 片渕竜也
目次
1. はじめに
本章では散乱現象の量子力学的な取り扱いについて説明する。散乱の量子力学は、核反応データを理解する上で基礎となるものである。散乱現象では粒子の波としての性質が顕著に現れる。したがって、その記述には量子力学が必要となる。ここでは初級編としてあまり難しくならない範囲で散乱問題の基本概念について学び、さらに低エネルギーの散乱現象を取り扱う際に有用な部分波展開と位相のずれについて説明する。2. 散乱問題
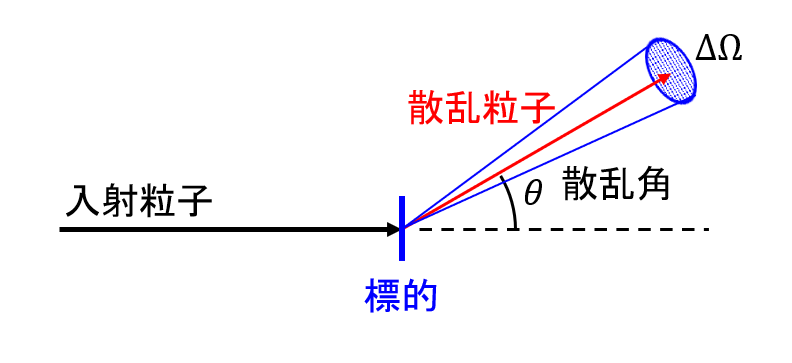
図1 散乱問題
3. 散乱問題の境界条件
ここでは散乱問題の導入として、最も基本となる弾性散乱を考える。散乱問題を量子力学的に扱うとは、すなわちそのシュレーディンガー方程式を解くことである。シュレーディンガー方程式を解くにはまず境界条件を与える必要がある。束縛問題では波動関数が無限遠方でゼロになるとし波動関数は空間的に閉じ込められたものとなった。そして、その結果、取りうるエネルギーが離散的になった。一方、散乱問題では粒子は空間的に閉じ込められていない。したがって、取り得るエネルギーは連続的になり、どんな値も許される。散乱実験において入射粒子のエネルギーは加速器の電圧により決められているように散乱問題において入射粒子の運動エネルギーは条件として与えられる。まず、入射粒子の波動関数を考えよう。入射粒子は\(z\)軸方向に一定の運動エネルギー\(E\)で進行するとする。このとき、入射粒子の波動関数\(u\)は次の1次元のシュレーディンガー方程式を満たす。
\begin{align} E u = -\frac{\hbar^2}{2 m} \frac{d^2 u}{d z^2} \tag{3.1} \end{align} ここで\(m\)は入射粒子の質量である。このシュレーディンガー方程式を解くと
\begin{align} u(z) &= e^{ikz} \tag{3.2} \\ k &= \frac{\sqrt{2 m E}}{\hbar} \tag{3.3} \end{align} という解が得られる注1。これは波長\(\lambda = 2\pi/k\)の平面波である。
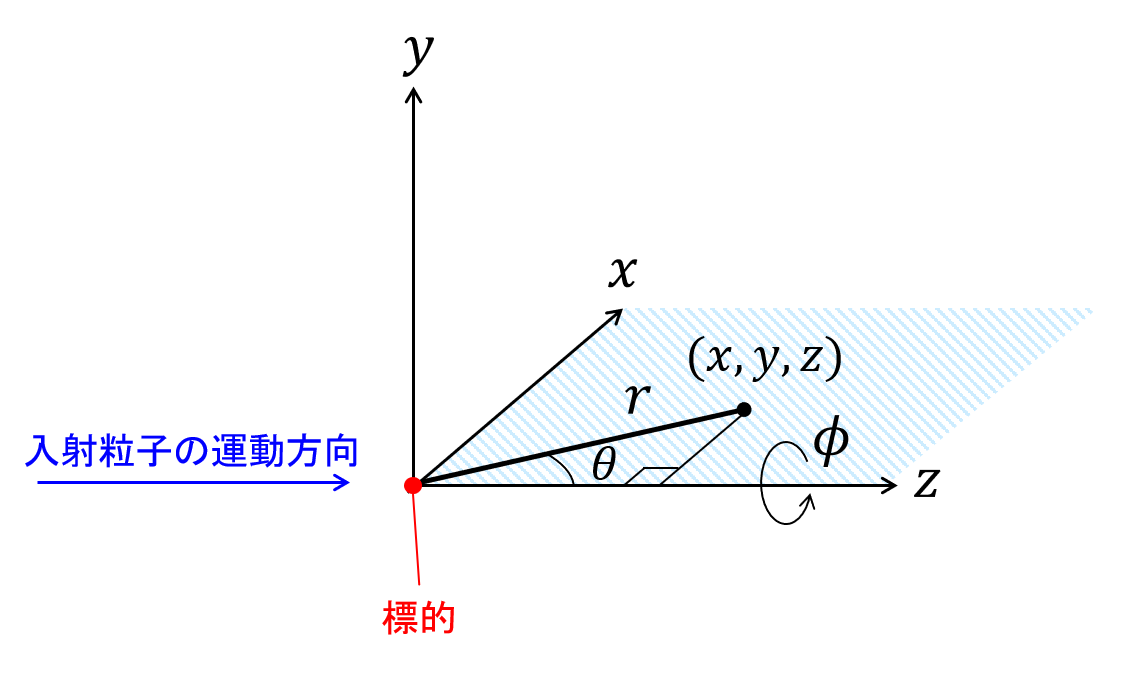
図2 球面極座標系の定義
\begin{align} E\Psi(\boldsymbol{r}) &=-\frac{\hbar^2}{2m}\left(\frac{\partial^2\Psi(\boldsymbol{r})}{\partial x^2}+\frac{\partial^2\Psi(\boldsymbol{r})}{\partial y^2}+\frac{\partial^2\Psi(\boldsymbol{r})}{\partial z^2}\right) \tag{3.4} \end{align} である。
第1章で示したようにハミルトニアンを球面極座標系で表すと次のようになる(散乱問題は球面極座標を採用する方が便利である)。図2に示すように入射粒子の運動方向を\(z\)軸と定義する。
\begin{align} E\Psi(r, \theta, \phi) = -\frac{\hbar^2}{2m}\left(\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r}) +\frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) \Psi(r, \theta, \phi) \tag{3.5} \end{align} 第1章で見たようにこの方程式は変数分離できる。動径成分のみの方程式を書き下すと
\begin{align} E R(r) & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}(r^2\frac{d}{d r}) R(r) \tag{3.6} \end{align} となる。ここで
\begin{align} R(r)= \frac{v(r)}{r} \tag{3.7} \end{align} とおいて、式(3.6)に代入すると
\begin{align} E \frac{v}{r} & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}\left(r^2\frac{d}{d r}(\frac{v}{r})\right)\\ & = -\frac{\hbar^2}{2m}\frac{1}{r}\frac{d^2 v}{dr^2}\\ \therefore E v & = -\frac{\hbar^2}{2m}\frac{d^2 v}{dr^2} \tag{3.8} \end{align} となり、式(3.1)と全く同じ形の方程式となる。したがって、\(v(r)\)は
\begin{align} v(r)= e^{ikr} \tag{3.9} \end{align} となり、波動関数の動径成分は
\begin{align} R(r)= \frac{e^{ikr}}{r} \tag{3.10} \end{align} となる注2。これは外向き球面波を表す。

図3 散乱の境界条件
\begin{align} \frac{f(\theta) e^{ikr}}{r} \tag{3.11} \end{align} となる。
以上の結果から、標的ポテンシャルから十分離れた場所での波動関数は
\begin{align} \Psi(r,\theta) \rightarrow e^{ikz} + \frac{f(\theta) e^{ikr}}{r} \tag{3.12} \end{align} となる。入射波成分\(e^{ikz}\)と散乱波の動径成分\(e^{ikr}/r\)はエネルギーを決めれば自ずと決まってしまうので散乱問題とはすなわち\(f(\theta)\)を求める問題と言ってよい。\(f(\theta)\)は散乱振幅と呼ばれる。
(断面積と散乱振幅の関係)散乱実験においては散乱粒子を検出器で測定する。散乱角\(\theta\)、距離\(r\)、面積\(S\)の検出器に入ってくる散乱粒子の確率\(P_s\)は、波動関数の散乱成分の絶対値の二乗に面積を乗じたものなので
\begin{align} P_s = \frac{|f(\theta)|^2}{r^2}S \tag{3.13} \end{align} である。ここで入射波は検出器には入ってこないとしている注3。
検出器の標的に対する立体角を\(\Delta\Omega\)とすると面積は\(S = r^2 \Delta\Omega\)なので
\begin{align} P_s &= \frac{|f(\theta)|^2}{r^2}r^2 \Delta\Omega\\ &= |f(\theta)|^2\Delta\Omega \tag{3.14} \end{align} となる。\(|f(\theta)|^2\)は、立体角あたりに検出する粒子の数なので、これは微分断面積にほかならない。すなわち
\begin{align} \frac{d \sigma}{d \Omega} = |f(\theta)|^2 \tag{3.15} \end{align} である。また、全立体角について積分すると全断面積が得られる。
\begin{align} \sigma = \int |f(\theta)|^2 d\Omega \tag{3.16} \end{align} 以上のことから、\(f(\theta)\)が求まれば、断面積が求まる。
4. 散乱問題のシュレーディンガー方程式と積分方程式
簡単のために中心力ポテンシャルのみ扱う。すなわちポテンシャル\(V\)は原点からの距離のみに依存する。このとき、シュレーディンガー方程式は球面極座標表示で次のように書ける。\begin{align} E\Psi(r, \theta, \phi) = -\frac{\hbar^2}{2m}\left(\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r}) +\frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial}{\partial\theta}) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right) \Psi(r, \theta, \phi) + V(r) \Psi(r, \theta, \phi) \tag{3.17} \end{align} 式(3.12)の散乱の境界条件をもとで式(3.17)を解くと次の解が得られる。
\begin{align} \Psi(\boldsymbol{r}) = e^{ikz} -\frac{2m}{4 \pi \hbar^2}\int \frac{\exp(i k|\boldsymbol{r}-\boldsymbol{r'}|)}{|\boldsymbol{r}-\boldsymbol{r'}|}V(r')\Psi(\boldsymbol{r'})d^3\boldsymbol{r'} \tag{3.18} \end{align} この解の導出は初級編のレベルを超えるので結果のみを記す。興味のある読者は参考文献を参照してほしい文献1。ここでは式(3.18)の物理的な意味についてのみ考察する。
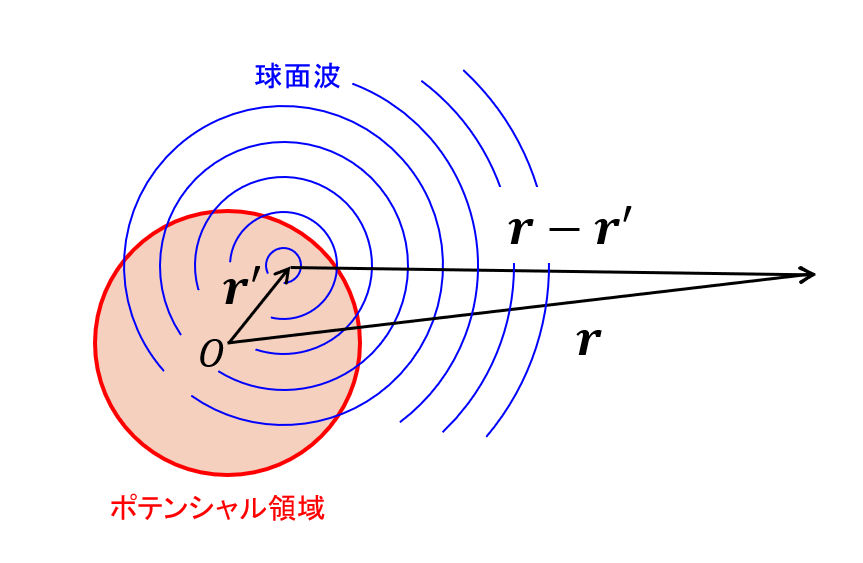
図4 点\(\boldsymbol{r'}\)で生じた球面波
\begin{align} \frac{\exp(i k|\boldsymbol{r}-\boldsymbol{r'}|)}{|\boldsymbol{r}-\boldsymbol{r'}|} \tag{3.19} \end{align} は、点\(\boldsymbol{r'}\)で生じた球面波である(図4)。すなわち、式(3.18)の右辺第2項はポテンシャルがゼロではない領域で生じた全ての球面波を重ね合わせたものが散乱波となることを意味している。また、各点の散乱の度合いはポテンシャルの大きさと確率振幅の積\(V(r')\Psi(\boldsymbol{r'})\)に比例する。
式(3.18)の無限遠方での漸近形を求めてみよう。\(r \gg r'\)とすると
\begin{align} |\boldsymbol{r}-\boldsymbol{r'}| &= \sqrt{r^2+r'^2-2(\boldsymbol{e_r}\cdot\boldsymbol{r'})r} \\ & \approx r- \boldsymbol{e_r}\cdot\boldsymbol{r'} \tag{3.20} \\ \frac{1}{|\boldsymbol{r}-\boldsymbol{r'}|} &= \frac{1}{\sqrt{r^2+r'^2-2(\boldsymbol{e_r}\cdot\boldsymbol{r'})r}}\\ & \approx r^{-1}(1+ \frac{\boldsymbol{e_r}\cdot\boldsymbol{r'}}{r}) \\ & \approx \frac{1}{r} \tag{3.21} \end{align} となる。ここで\(\boldsymbol{e_r}\)は\(\boldsymbol{r}\)方向の単位ベクトルである。これらの結果を式(3.19)に代入すると
\begin{align} \frac{\exp(i k|\boldsymbol{r}-\boldsymbol{r'}|)}{|\boldsymbol{r}-\boldsymbol{r'}|} &\rightarrow \frac{\exp\{ik(r- \boldsymbol{e_r}\cdot\boldsymbol{r'})\}}{r}\\ & = \frac{e^{ikr} \exp(-i\boldsymbol{k'}\cdot\boldsymbol{r'})}{r} \tag{3.22} \end{align} となる。ここで\(\boldsymbol{k'}=k\boldsymbol{e_r}\)は散乱方向の波数ベクトルである。
式(3.22)から式(3.18)の無限遠での漸近型は
\begin{align} \Phi(\boldsymbol{r}) \rightarrow e^{ikz} + \frac{e^{ikr}}{r}\left( -\frac{2m}{4 \pi \hbar^2}\int \exp(-i \boldsymbol{k'}\cdot\boldsymbol{r'})V(r')\Phi(\boldsymbol{r'})d^3\boldsymbol{r'}\right) \tag{3.23} \end{align} となる。第2項の括弧の中が散乱振幅に相当するので
\begin{align} f(\theta) = -\frac{2m}{4 \pi \hbar^2}\int \exp(-i \boldsymbol{k'}\cdot\boldsymbol{r'})V(r')\Phi(\boldsymbol{r'})d^3\boldsymbol{r'} \tag{3.24} \end{align} である。
(ボルン近似)原理的には積分方程式(3.18)を解いて\(\Psi(\boldsymbol{r})\)が求まれば、式(3.24)から散乱振幅が計算でき、さらに式(3.16)から断面積も計算することができる。しかし、実際にはほとんどの場合、方程式(3.18)を解いて\(\Psi(\boldsymbol{r})\)を直接求めることはできない。そこで近似的な手法を用いることになる。
よく行われる最も簡単な近似方法は、式(3.18)の右辺第2項は第1項に比べ小さいとして、積分の中の\(\Psi(\boldsymbol{r})\)を第1項の入射波で代用してしまう方法である。つまり
\begin{align} \Phi(\boldsymbol{r}) \approx e^{ikz} \tag{3.25} \end{align} として、これを式(3.24)に代入し
\begin{align} f(\theta) = -\frac{2m}{4 \pi \hbar^2}\int \exp(-i \boldsymbol{k'}\cdot\boldsymbol{r'})V(r')\exp(ikz')d^3\boldsymbol{r'} \tag{3.26} \end{align} とすれば、この積分は容易に実行でき、散乱振幅\(f(\theta)\)を計算することができる。この近似法をボルン近似と呼ぶ。
ボルン近似は式(3.25)の仮定が素朴すぎるため計算結果は実際の実験結果を再現できないことが多いが、計算が簡単なため散乱問題を扱うときに最初に試してみる近似法としてよく用いられる。
5. 部分波展開と位相のずれ
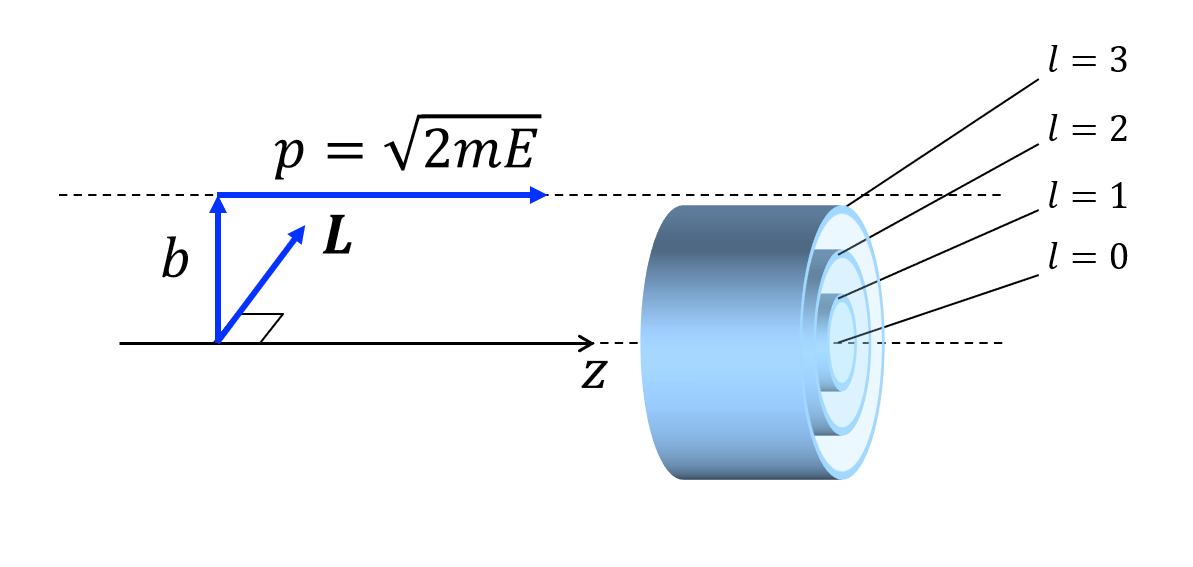
図5 入射波の部分波成分
\begin{align} \boldsymbol{L} = \boldsymbol{r} \times \boldsymbol{p} \tag{3.27} \end{align} 入射粒子の運動エネルギーは、\(E\)として与えられているので運動量の大きさ\(p\)は
\begin{align} p = \sqrt{2 m E} \end{align} となる。図5に示すように入射粒子の軌道と\(z\)軸の距離を\(b\)とすれば、軌道角運動量の大きさ\(L\)は
\begin{align} L = b p =b \sqrt{2 m E} \tag{3.28} \end{align} となる。また、波数\(k\)(\(= 2\pi/\lambda = p/\hbar\))を用いると
\begin{align} L = \hbar k b \tag{} \end{align} である。
\(p\)は定数なので式(3.28)から入射粒子の軌道角運動量は\(z\)軸からの距離\(b\)により決まることが分かる。\(b\)は衝突パラメータとも呼ばれる。\(b\)が大きいほどすなわち\(z\)軸から外側に行くほど軌道角運動量は大きくなる。
さらに量子力学では、第1章で述べたように軌道角運動量はとびとびの値を取る。すなわち、\(l\)を整数としたとき、軌道角運動量は\(L = l \hbar\)となる。したがって、入射粒子の空間分布は図2に示すように内側から\(l=0, 1, 2, \cdots\)と同心円状の分布となる。平面波は異なる軌道角運動量成分を含むことから、次のように平面波を軌道角運動量の固有関数の重ね合わせとして表すことができる(レイリー展開)。
\begin{align} e^{ikz} &= e^{i k r \cos \theta} \\ &= \sum_{l=0}^{\infty} (2l+1)i^{l}j_l(kr)P_l(\cos \theta) \tag{3.29} \\ &= j_0(kr)P_0(\cos \theta) + 3i j_1(kr)P_1(\cos \theta) - 5 j_2(kr)P_2(\cos \theta) + \cdots \tag{3.30} \end{align} 各項はそれぞれ\(l=0, 1, 2, \cdots\)の波動関数成分を表している。それぞれの軌道角運動量成分を部分波と呼び、式(3.29)の展開を部分波展開と呼ぶ。ここで\(j_l(kr)\)は球ベッセル関数と呼ばれる特殊関数注5であり、波動関数の動径方向の依存性を表している。ポテンシャルのない自由空間でのシュレーディンガー方程式の解となっている。すなわち次の動径成分のシュレーディンガー方程式を満たす。
\begin{align} k^2 j_l(kr) & = \left(-\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{l(l+1)}{r^2}\right)j_l(kr) \tag{3.31} \end{align} また、\(P_l(\cos \theta)\)は、ルジャンドル多項式であり、軌道角運動量が\(l \hbar\)の時の固有関数である。第1章で軌道角運動量の大きさが\(l\hbar\)、\(z\)成分が\(m\hbar\)の時の波動関数は次の球面調和関数で与えられることを述べた。
\begin{align} Y_{l m}(\theta,\phi)= i^{m+|m|}\left(\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}\right)P_{l m}(\cos\theta)e^{im\phi} \tag{3.32} \end{align} 図2に示すように入射粒子の運動方向を\(z\)軸とした時、軌道角運動量の方向はz軸に常に直交している。したがって、軌道角運動量の\(z\)成分は常にゼロである。すなわち\(m=0\)である。したがって、平面波の部分波展開には\(m \neq 0\)の成分は含まれない。\(m=0\)のとき、式(3.32)は
\begin{align} Y_{l 0}(\theta,\phi) &= \left(\frac{2l+1}{4\pi}\right)P_{l 0}(\cos\theta)\\ & = \left(\frac{2l+1}{4\pi}\right)P_{l}(\cos\theta) \tag{3.33} \end{align} となり、式(3.29)の展開に現れている\(P_l(\cos \theta)\)が、\(m=0\)の波動関数であることが分かる。
部分波展開を用いると問題を軌道角運動量ごとに分けて扱うことができる。ポテンシャルが中心力の場合には軌道角運動量は保存するので入射波と散乱波の軌道角運動量は等しくなり特に簡単になる。また、式(3.28)の衝突パラメータ\(b\)が原子核半径程度までのものしか散乱には寄与しない。したがって、運動エネルギーが低いときには小さな軌道角運動量のだけを考えればよく、問題が簡単になる。特に低エネルギーの中性子の散乱を考える場合には、主に\(l=0\)、もしくはせいぜい\(l=1\)まで考慮すれば十分である。
球ベッセル関数は無限遠方では次のような正弦波の形になる。
\begin{align} j_l(kr) &\rightarrow \frac{\sin(kr-l\pi /2)}{kr} \tag{3.34} \end{align} したがって、式(3.29)の無限遠方での漸近形は次のようになる注6。
\begin{align} e^{ikz} &\rightarrow \frac{1}{kr}\sum_{l=0}^{\infty} (2l+1)i^{l} \sin(kr-l\pi /2)P_l(\cos \theta) \tag{3.35} \\ &= \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \left(e^{ikr}-(-1)^l e^{-ikr} \right) P_l(\cos \theta) \tag{3.36} \\ \end{align}

図6 波動関数の動径成分の3つの領域
まず、散乱振幅\(f(\theta)\)をルジャンドル多項式\(P_{l}(\cos\theta)\)で展開することで散乱波を部分波に分解する。すなわち
\begin{align} f(\theta) = \frac{1}{2ik} \sum_{l=0}^{\infty} (2l+1) b_l P_l(\cos \theta) \tag{3.37} \\ \end{align} と表す。ここで\(b_l\)は、\(l\)ごとの展開係数である。以後の計算を簡単にするために式(3.36)に合わせて因子\((2l+1)/2ik\)を係数\(b_l\)から取り出してある。式(3.36)と式(3.37)を波動関数の無限遠方での境界条件すなわち式(3.12)に代入すると
\begin{align} \Psi(r,\theta) &\rightarrow e^{ikz} + \frac{f(\theta) e^{ikr}}{r} \\ &= \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \left(e^{ikr}-(-1)^l e^{-ikr} \right) P_l(\cos \theta) + \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) b_l e^{ikr} P_l(\cos \theta)\\ &= \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \{(1+b_l)e^{ikr}-(-1)^l e^{-ikr} \} P_l(\cos \theta) \\ &= \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \{e^{2i\delta_l}e^{ikr}-(-1)^l e^{-ikr} \} P_l(\cos \theta) \tag{3.38} \end{align}
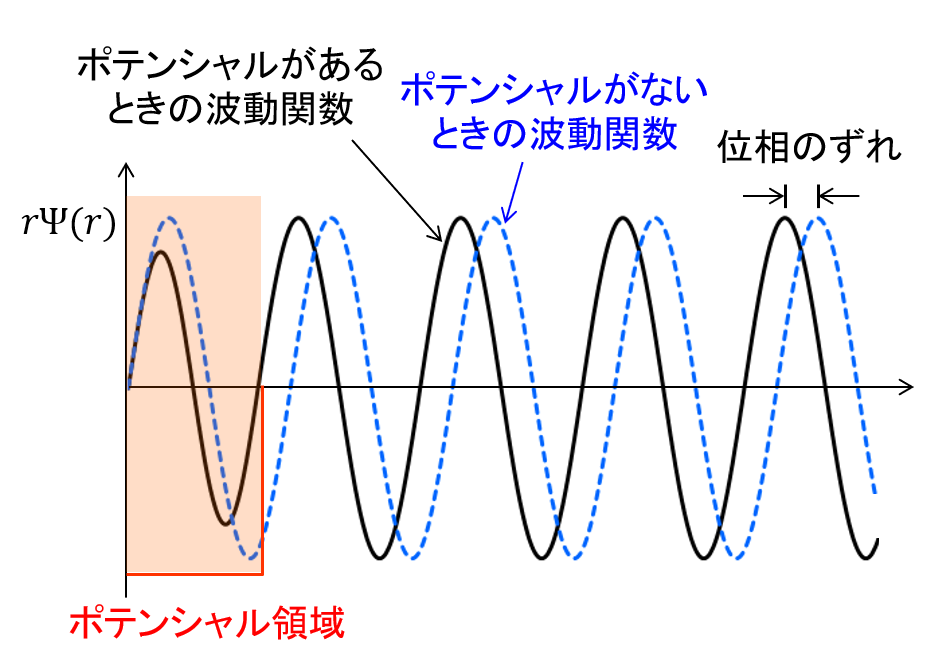
図7 位相のずれ
\begin{align} b_l = e^{2i\delta_l} - 1 \tag{3.39} \end{align} 新しく導入した\(\delta_l\)は、位相のずれ(phase shift)と呼ばれる。その理由は、式(3.38)の括弧内を変形してみると分かる。
\begin{align} &e^{2i\delta_l} e^{ikr}-(-1)^l e^{-ikr}\\ &= i^l e^{i\delta_l}\{ (-i)^l e^{i(kr+\delta_l)}-(i)^l e^{-i(kr+\delta_l)}\} \\ &= i^l e^{i\delta_l}\{ e^{i(kr-l\pi /2+\delta_l)}-e^{-i(kr-l\pi /2+\delta_l)}\} \\ &= 2i\cdot i^l e^{i\delta_l}\sin(kr-l\pi /2+\delta_l) \tag{3.40} \end{align} これを式(3.38)に代入すると
\begin{align} \Psi(r,\theta) &\rightarrow \frac{1}{kr} \sum_{l=0}^{\infty} (2l+1) i^l e^{i\delta_l}\sin(kr-l\pi /2+\delta_l) P_l(\cos \theta) \tag{3.41} \end{align} となる。入射平面波の漸近式(3.35)と比較すると位相が\(\delta_l\)だけ異なっていることが分かる。これは図7に示すようにポテンシャル内では引力の場合、波動関数の波長は短くなり、その分、外部波動関数が引き込まれ、結果として正の位相のずれが生じる。逆に斥力の場合、ポテンシャル内で波長は長くなるので位相のずれは負となる。
位相のずれを用いる最大の利点は、軌道角運動量\(l\)の部分波の散乱は位相のずれ\(\delta_l\)という一つの量に集約されることである。位相のずれが分かると断面積などの物理量を計算することができる。
ちなみにポテンシャルの外の波動関数を位相のずれを用いると以下のように表される。実際、無限遠方では漸近形が式(3.41)と一致することからこの式が正しいことが分かる注7。
\begin{align} \Psi(r,\theta) = \sum_{l=0}^{\infty} (2l+1) i^l e^{i\delta_l}\left(\cos\delta_l j_l(kr) - \sin\delta_l n_l(kr)\right) P_l(\cos \theta) \tag{3.42} \end{align} ここで\(n_l(kr)\)は球ノイマン関数である注5。球ノイマン関数は球ベッセル関数と同様に方程式(3.31)を満たす解である。ただし、球ベッセル関数が\(r=0\)で正則であるのに対し、球ノイマン関数は\(r=0\)で正則ではない解である。球ノイマン関数の無限遠方での漸近形は
\begin{align} n_l(kr) &\rightarrow -\frac{\cos(kr-l\pi /2)}{kr} \tag{3.43} \end{align} となる。
(断面積との関係)位相のずれが与えられれば断面積を計算することができる。式(3.37)と式(3.39)から散乱振幅は位相のずれにより次のように表される。
\begin{align} f(\theta) &= \frac{1}{2ik} \sum_{l=0}^{\infty} (2l+1) (e^{2i\delta_l} - 1) P_l(\cos \theta) \\ &= \frac{1}{k} \sum_{l=0}^{\infty} (2l+1) e^{i\delta_l}\sin\delta_l P_l(\cos \theta) \tag{3.44} \end{align} 断面積は式(3.16)に与えられるように\(f(\theta)\)の絶対値の2乗を全立体角で積分すると求まる注8。
\begin{align} \sigma &= \int |f(\theta)|^2 d\Omega \\ &= \frac{1}{k^2} \int |\sum_{l=0}^{\infty} (2l+1) e^{i\delta_l}\sin(\delta_l) P_l(\cos \theta)|^2 d\Omega \\ &= \frac{1}{k^2} \int_0^{\pi} |\sum_{l=0}^{\infty} (2l+1) e^{i\delta_l}\sin(\delta_l) P_l(\cos \theta)|^2 2 \pi \sin \theta d\theta \\ &= \frac{4\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) \sin^2\delta_l \tag{3.45} \end{align}
6. 位相のずれの決定
ポテンシャル内部の波動関数が分かると位相のずれ\(\delta_l\)を決定することができる。ポテンシャルを\(V(r)\)としたとき、軌道角運動量\(l\)を持つ波動関数の動径成分のシュレーディンガー方程式は第1章の式(1.88)から次のようになる。\begin{align} E R_l(r) & = \left(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}(r^2\frac{d}{d r})+\frac{l(l+1)\hbar^2}{2 m r^2}+ V(r)\right)R_l(r) \tag{3.46} \end{align} 与えられたポテンシャル\(V(r)\)についてこの方程式の解\(R_l\)が、解析解でも数値解でも構わないので得られれば、\(\delta_l\)を決めることができる。
位相のずれ\(\delta_l\)の決定には連続の条件を用いる。ポテンシャル内部の波動関数および外部の波動関数の動径成分をそれぞれ\(v_l(r)\)、\(u_l(r)\)とするとポテンシャル表面(\(r = a\))において連続的に接続しなくてはならないことから
\begin{align} v_l(a)= u_l(a) \tag{3.47} \end{align} である。また、その微分係数も連続的に接続しなければならない注9。つまり
\begin{align} \left. \frac{d v_l}{dr}\right|_{r=a} = \left. \frac{d u_l}{dr}\right|_{r=a} \tag{3.48} \end{align} である。式(3.47)と(3.48)の条件は次のように一つの式で表すことができる(対数微分とも言う)注10。
\begin{align} \left. \frac{1}{v_l}\frac{d v_l}{dr}\right|_{r=a} = \left. \frac{1}{u_l}\frac{d u_l}{dr}\right|_{r=a} \tag{3.49} \end{align} ここで式(3.42)からポテンシャルの外部関数の動径成分は\(\delta_l\)を用いて次のように書ける。
\begin{align} u_l(r) = \cos\delta_l j_l(kr) - \sin\delta_l n_l(kr) \tag{3.50} \end{align} したがって、\(u_l\)の対数微分は \begin{align} \left. \frac{1}{u_l}\frac{d u_l}{dr}\right|_{r=a} = \frac{k[\cos\delta_l j'_l(ka) - \sin\delta_l n'_l(ka)]}{\cos\delta_l j_l(ka) - \sin\delta_l n_l(ka)} \tag{3.51} \end{align} となる。\(j'_l\)と\(n'_l\)はそれぞれ球ベッセル関数と球ノイマン関数の微分形である。ここで次のように内部波動関数の対数微分を\(\gamma_l\)とおけば、
\begin{align} \gamma_l = \left. \frac{1}{v_l}\frac{d v_l}{dr}\right|_{r=a} \tag{3.52} \end{align} 式(3.52)の条件式は次のように書き直せる。
\begin{align} \gamma_l = \frac{k[\cos\delta_l j'_l(ka) - \sin\delta_l n'_l(ka)]}{\cos\delta_l j_l(ka) - \sin\delta_l n_l(ka)} \tag{3.53} \end{align} この式を\(\delta_l\)について解くと
\begin{align} \tan \delta_l = \frac{k j'_l(ka) - \gamma_l j_l(ka)}{k n'_l(ka) - \gamma_l n_l(ka)} \tag{3.54} \end{align} が得られ、内部波動関数のポテンシャル表面の微分係数\(\gamma_l\)から位相のずれ\(\delta_l\)を求めることができる。位相のずれを求め断面積を計算するまでの一連の流れを図8に示す。
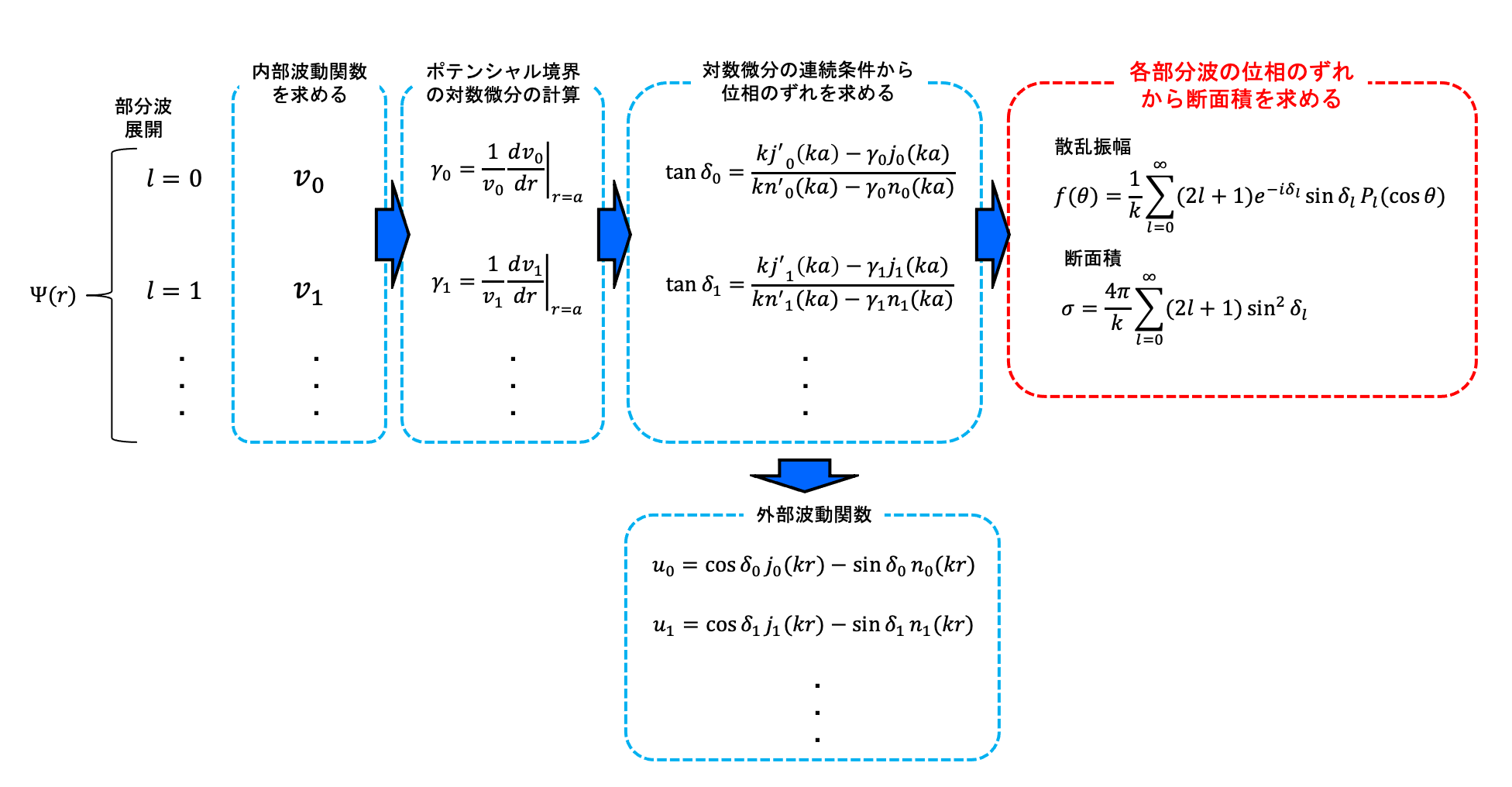
図8 位相のずれを決定し断面積を求める手順
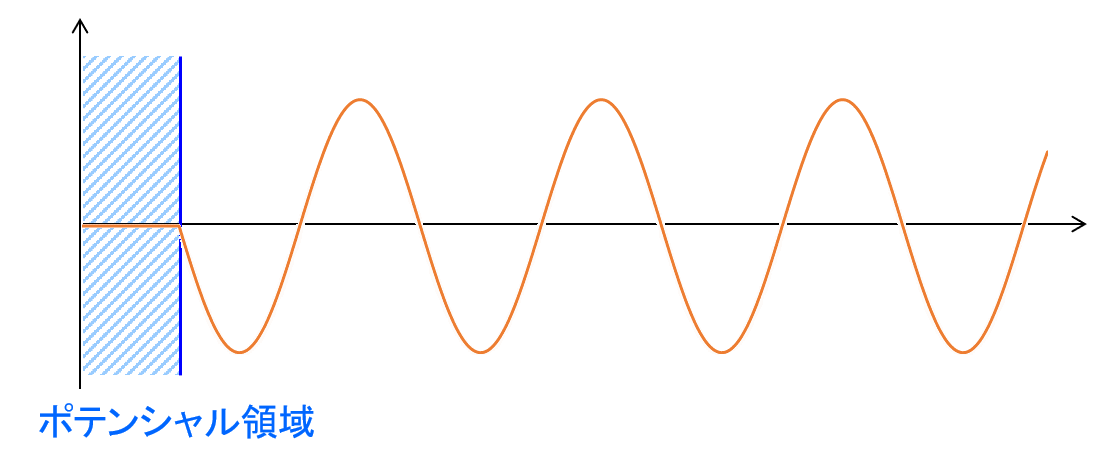
図9 完全剛体球の波動関数
(完全剛体球)ポテンシャルが無限の高さの斥力ポテンシャルの場合、粒子はポテンシャル内部に侵入できず波動関数はゼロとなる。容易に想像されるように入射粒子はポテンシャル表面で完全反射される。このようなポテンシャルを完全剛体球ポテンシャルとよぶ。このとき、ポテンシャル表面\(r = a\)で波動関数はゼロとなり、式(3.53)の対数微分\(\gamma_l\)は無限大となる。つまり
\begin{align} v_l(a) &= 0 \tag{3.55}\\ \gamma_l &= \left. \frac{1}{v_l}\frac{d v_l}{dr}\right|_{r=a} = \infty \tag{3.56} \end{align} である。したがって、式(3.54)は
\begin{align} \tan \delta_l &= \frac{k j'_l(ka) - \gamma_l j_l(ka)}{k n'_l(ka) - \gamma_l n_l(ka)} \\ &= \frac{k j'_l(ka)/\gamma_l - j_l(ka)}{k n'_l(ka)/\gamma_l - n_l(ka)} \\ &\xrightarrow[\gamma_l\to\infty]{} \frac{j_l(ka)}{n_l(ka)} \\ \therefore \; \tan \delta_l &= \frac{j_l(ka)}{n_l(ka)} \tag{3.57} \end{align} となる。
ここで入射粒子が低エネルギー(\(ka \ll 1\))の場合を扱う。\(kr \ll 1\)の場合、球ベッセル関数および球ノイマン関数は次のように近似できる注5。
\begin{align} j_l(kr) &\xrightarrow[kr\to 0]{} \frac{(kr)^l}{(2l+1)!!} \tag{3.58} \\ n_l(kr) &\xrightarrow[kr\to 0]{} -\frac{(2l-1)!!}{(kr)^{l+1}} \tag{3.59} \\ (2l+1)!! &\equiv 1\cdot3\cdot5\cdots(2l+1) \end{align} 式(3.57)に式(3.58), (3.59)を代入すると
\begin{align} \tan \delta_l &\approx \frac{j_l(ka)}{n_l(ka)} \\ &= - \frac{(ka)^l}{(2l+1)!!} \frac{(ka)^{l+1}}{(2l-1)!!} \\ &= - \frac{(ka)^{2l+1}}{(2l+1)[(2l-1)!!]^2} \tag{3.60} \end{align} となる。\(l=0, 1\)の場合を計算すると
\begin{align} \tan \delta_0 &= - ka \tag{3.61} \\ \tan \delta_1 &= - \frac{(ka)^3}{3} \tag{3.62} \\ \end{align} が得られる。式(3.43)にあるように断面積の計算には\(\sin^2\delta\)が必要なので計算すると
\begin{align} \sin^2 \delta_0 &= \frac{\tan^2\delta_0}{\tan^2\delta_0 + 1} \\ &= \frac{(ka)^2}{(ka)^2 + 1} \approx (ka)^2 \tag{3.63} \\ \sin^2 \delta_1 &= \frac{(ka)^6}{(ka)^6 + 9} \approx \frac{(ka)^6}{9} \tag{3.64} \\ \end{align} となる。\(l=2\)以上も同様に計算できて軌道角運動量\(l\)の部分波の\(\sin^2 \delta_l\)は、\((ka)^{4l+2}\)のオーダである。式(3.43)により断面積は
\begin{align} \sigma &= \frac{4\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) \sin^2\delta_l \\ &\approx \frac{4\pi}{k^2} \left( (ka)^2 + 3 \cdot \frac{(ka)^6}{9} \cdots \right)\\ &= 4\pi \left( a^2 + \frac{k^4a^6}{3} \cdots \right) \tag{3.65} \end{align}

図10 \(l=0\)の内向き球面波
\begin{align} \sigma \approx 4\pi a^2 \tag{3.66} \end{align} となる。結果から分かるように完全剛体球の場合、断面積は幾何学的断面積\(\pi a^2\)の4倍となる。この4倍になる理由は次のように考えると理解できる。すなわち\(l=0\)の部分波は、等方的な球面波である。入射波はあらゆる方向から内向き球面波として球対称にポテンシャル表面に当たる(図10)。その結果、断面積はポテンシャルの表面積\(4\pi a^2\)となる。
(井戸型ポテンシャル)次にポテンシャルの深さが有限の井戸型ポテンシャルを考えてみよう。
\begin{align} V(r) = \left\{ \begin{array}{ll} -V_0 & (r \leq a) \tag{3.67}\\ 0 & (r \gt a) \end{array} \right. \end{align} ポテンシャルの中でのシュレーディンガー方程式は以下のようになる。
\begin{align} E R_l(r) & = \left(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}(r^2\frac{d}{d r})+\frac{l(l+1)\hbar^2}{2 m r^2}- V_0\right)R_l(r) \tag{3.68} \end{align} 書き直すと
\begin{align} \frac{1}{r^2}\frac{d}{d r}(r^2\frac{d R_l(r)}{d r})-\frac{l(l+1)}{r^2}R_l(r)+\frac{2 m (E + V_0)}{\hbar^2} R_l(r) = 0 \tag{3.69} \end{align} となり、以下で定義する\(\alpha\)を導入すると
\begin{align} \alpha = \sqrt{ \frac{2 m (E + V_0)}{\hbar^2}} \tag{3.70} \end{align} シュレーディンガー方程式(3.69)は
\begin{align} \frac{1}{r^2}\frac{d}{d r}(r^2\frac{d R_l(r)}{d r})-\frac{l(l+1)}{r^2}R_l(r)+ \alpha^2 R_l(r) = 0 \tag{3.71} \end{align} となる。この方程式の解は球ベッセル関数\(j_l\)であり、以下のように書ける。
\begin{align} R_l(r) = B_l j_l(\alpha r) \tag{3.72} \end{align} ここで\(B_l\)は係数である。
位相のずれを決定するにはポテンシャル表面の接続条件から導かれた式(3.55)から求める。すなわち
\begin{align} \tan \delta_l = \frac{k j'_l(ka) - \gamma_l j_l(ka)}{k n'_l(ka) - \gamma_l n_l(ka)} \tag{3.73} \end{align} である。
完全剛体球の場合と同様に非常に低エネルギーの場合(\(ka \ll 1\))について考察する。式(3.59)、(3.60)に示したように\(kr\)が小さいときには次のように近似できる。
\begin{align} j_l(kr) &\xrightarrow[kr\to 0]{} \frac{(kr)^l}{(2l+1)!!} \tag{3.74} \\ n_l(kr) &\xrightarrow[kr\to 0]{} -\frac{(2l-1)!!}{(kr)^{l+1}} \tag{3.75} \\ (2l+1)!! &\equiv 1\cdot3\cdot5\cdots(2l+1) \end{align} これらの微分型を計算すると
\begin{align} j'_l(kr) &\xrightarrow[kr\to 0]{} \frac{lk(kr)^{l-1}}{(2l+1)!!} \tag{3.76} \\ n'_l(kr) &\xrightarrow[kr\to 0]{} \frac{(l+1)(2l-1)!!}{(kr)^{l+2}} \tag{3.77} \\ \end{align} となる。これらを式(3.73)に代入すると
\begin{align} \tan \delta_l &= \frac{k j'_l(ka) - \gamma_l j_l(ka)}{k n'_l(ka) - \gamma_l n_l(ka)}\\ &\approx \frac{1}{(2l+1)!!(2l-1)!!} \frac{lk^2(ka)^{l-1} - \gamma_l(ka)^l}{k(l+1) (ka)^{-(l+2)} + \gamma_l(ka)^{-(l+1)}} \\ &= \frac{(ka)^{2l+1}}{(2l+1)!!(2l-1)!!} \frac{l - \gamma_l a}{l+1 + \gamma_l a} \tag{3.78} \end{align} となる。低次の\(l =0, 1\)の場合について計算すると
\begin{align} \tan \delta_0 &= -\frac{\gamma_0 k a}{1+\gamma_0 a} \tag{3.79} \\ \tan \delta_1 &= - \frac{(ka)^3}{3}\frac{1-\gamma_1 a}{2+\gamma_1 a} \tag{3.80} \\ \end{align} となる。\(\gamma_0 a =-1\) または \(\gamma_1 a = -2\)の場合を除けば、式(3.79), (3.80)は\(k \rightarrow 0\)のときゼロになる。ただし、断面積を計算する場合には剛体球の場合の式(3.65)で見たように\(l=0\)の部分波成分だけは分母の因子\(1/k^2\)と打ち消し合うためゼロにはならない。すなわち
\begin{align} \sigma &= \frac{4\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) \sin^2\delta_l \\ &\approx \frac{4\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) \tan^2\delta_l \\ &= \frac{4\pi}{k^2} \left( \left(\frac{\gamma_0a}{1+\gamma_0 a}\right)^2(ka)^2 + 3 \cdot \left(\frac{1-\gamma_1 a}{2+\gamma_1 a}\right)^2 \frac{(ka)^6}{9} \cdots \right)\\ &= 4\pi \left( \left(\frac{\gamma_0 a}{1+\gamma_0 a}\right)^2 a^2 + \left(\frac{1-\gamma_1 a}{2+\gamma_1 a}\right)^2 \frac{k^4a^6}{3} \cdots \right) \\ &\xrightarrow[k\to 0]{} 4\pi a^2 \left(\frac{\gamma_0 a}{1+\gamma_0 a}\right)^2 \tag{3.81} \end{align} となる。\(\gamma_0\)は内部波動関数が球ベッセル関数なので直接求めることができる。すなわち
\begin{align} j_0(\alpha r) &= \frac{\sin \alpha r}{\alpha r} \tag{3.82}\\ j'_0(\alpha r) &= \frac{\cos \alpha r}{\alpha r} - \frac{\sin \alpha r}{(\alpha r)^2} \tag{3.83} \\ \end{align} である。\(\gamma_l\)の定義から
\begin{align} &\gamma_0 = \frac{\alpha j'_0(\alpha a)}{j_0(\alpha a)} \tag{3.84} \\ &\therefore \gamma_0 j_0(\alpha a) =\alpha j'_0(\alpha a) \tag{3.85} \\ \end{align} である。これに式(3.79), (3.80)を代入すると
\begin{align} \gamma_0 \left(\frac{\sin \alpha a}{\alpha a}\right) &=\alpha \left(\frac{\cos \alpha a}{\alpha a} - \frac{\sin \alpha a}{(\alpha a)^2}\right) \\ \therefore \gamma_0 a &= \frac{\alpha a}{\tan \alpha a} - 1 \tag{3.86} \\ \end{align} が得られる。これを式(3.81)に代入して
\begin{align} \sigma &\approx 4\pi a^2 \left(\frac{\gamma_0 a}{1+\gamma_0 a}\right)^2 \\ &= 4\pi a^2 \left[\left(\frac{\alpha a}{\tan \alpha a} - 1\right) \frac{\tan \alpha a}{\alpha a}\right]^2 \\ &= 4\pi a^2 \left(1 - \frac{\tan \alpha a}{\alpha a}\right)^2 \tag{3.87} \end{align} となる。剛体球の場合と同じように低ネルギーの散乱では\(l=0\)の部分波のみが寄与し、散乱は角度に依存せず等方的となる。
7. 反応断面積
ここまでの議論は弾性散乱のみを対象にして説明してきた。しかし、実際には第2章で述べたように捕獲反応や核分裂などいろいろな原子核反応が起きる。弾性散乱以外の原子核反応の断面積を合計したものを反応断面積と呼ぶ。この節では以下、反応断面積の取り扱いについて述べる。弾性散乱の波動関数の無限遠方での漸近形は、式(3.38)に示したように位相のずれを用いて次のように書くことができる。
\begin{align} \Psi(r,\theta) &\rightarrow \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \{e^{2i\delta_l}e^{ikr}-(-1)^l e^{-ikr} \} P_l(\cos \theta) \tag{3.88} \end{align} この式から分かるように波動関数の漸近形は内向き波\(e^{-ikr}\)と外向き波\(e^{ikr}\)の和として表される。弾性散乱しか起きない場合には、粒子数が保存するために内向き波と外向き波の振幅は等しくなければならない。実際、\(|e^{2i\delta_l}|=1\)である。しかし、弾性散乱以外の反応が起きると粒子は弾性散乱の外向き波として出てこないために外向き波の振幅は\(1\)より小さくなる。そこで式(3.88)の外向き波の振幅を\(S_l\)とおき、一般の場合に拡張する。\(S_l\)は複素数である。
\begin{align} \Psi(r,\theta) &\rightarrow \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \{S_le^{ikr}-(-1)^l e^{-ikr} \} P_l(\cos \theta) \tag{3.88} \end{align} 弾性散乱しか起きない場合には\(|S_l| = 1\)であり、反応が起きる場合には\(|S_l| < 1\)である。弾性散乱の場合と同じように位相のずれを導入すると\(S_l\)は次のように書ける。
\begin{align} S_l = |S_l| e^{2i\delta_l} \tag{3.89} \end{align} 弾性散乱の散乱振幅と断面積\(\sigma_s\)は式(3.44)、(3.45)の\(e^{2i\delta_l}\)を\(S_l\)で置き換えればよい。すなわち
\begin{align} f(\theta) &= \frac{1}{2ik} \sum_{l=0}^{\infty} (2l+1) (S_l - 1) P_l(\cos \theta) \tag{3.90}\\ \sigma_s &= \frac{\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) |1-S_l|^2 \tag{3.91} \end{align} となる注11。式(3.89)の位相のずれを用いて表すと
\begin{align} f(\theta) &= \frac{1}{2ik} \sum_{l=0}^{\infty} (2l+1) (|S_l| e^{2i\delta_l} - 1) P_l(\cos \theta) \tag{3.92}\\ \sigma_s &= \frac{\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) |1-|S_l| e^{2i\delta_l}|^2 \tag{3.93} \end{align} となる。
一方、反応断面積は、弾性散乱から失われた部分に相当する。したがって、内向き波と外向き波の振幅の絶対値の2乗の差 \(1-|S_l|^2\) が各部分波の反応断面積となる。このことから反応断面積\(\sigma_r\)は
\begin{align} \sigma_r &= \frac{\pi}{k^2} \sum_{l=0}^{\infty} (2l+1) (1-|S_l|^2) \tag{3.94} \end{align} となる。
注釈
- \(e^{-ikx}\)も式(3.1)の解だが、入射粒子の運動方向が逆向き(\(z\)軸の右から左)になるので除外する。
- 平面波の場合と同様に\(e^{-ikx}/r\)も解となるが、これは内向き球面波なので除外する。
- 通常の実験では検出器は標的から十分離れた位置に設置し入射粒子は検出器に入ってこないようにする。入射粒子の波動関数が無限に広がる平面波という仮定と矛盾するように聞こえるかもしれないが、典型的なビームサイズは、mmオーダーなので原子核の大きさから見れば十分平面波として近似できる。
- 途中計算は以下の通り。
\begin{align} E \frac{v}{r} & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}\left(r^2\frac{d}{d r}(\frac{v}{r})\right)\\ & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}\left(r^2(\frac{1}{r}\frac{dv}{dr}-\frac{v}{r^2})\right)\\ & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{d r}\left(r\frac{dv}{dr}-v\right)\\ & = -\frac{\hbar^2}{2m}\frac{1}{r^2}\left(\frac{dv}{dr}+r\frac{d^2 v}{dr^2}-\frac{dv}{dr}\right)\\ & = -\frac{\hbar^2}{2m}\frac{1}{r}\frac{d^2 v}{dr^2}\\ \therefore E v & = -\frac{\hbar^2}{2m}\frac{d^2 v}{dr^2} \end{align} - 以下、球ベッセル関数について簡単にまとめる。
球ベッセル関数は以下の方程式の解として与えられる。
\begin{align} \frac{d^2 j_l(\rho)}{d \rho^2}+\frac{2}{\rho}\frac{d j_l(\rho)}{d \rho}+\left[1-\frac{l(l+1)}{\rho^2}\right]j_l(\rho) = 0 \end{align} 最初の3つの球ベッセル関数を以下に示す。球ベッセル関数は\(\rho = 0\)で正則な関数である。
\begin{align} j_0(\rho) &= \frac{\sin \rho}{\rho} \\ j_1(\rho) &= \frac{\sin \rho}{\rho^2} - \frac{\cos \rho}{\rho} \\ j_2(\rho) &= \left(\frac{3}{\rho^3}-\frac{1}{\rho}\right)\sin \rho - \frac{3}{\rho^2}\cos \rho \end{align} 一方、\(\rho = 0\)で正則ではない方程式の解も存在し、球ノイマン関数と呼ばれる。最初の3つの球ノイマン関数を以下に示す。
\begin{align} n_0(\rho) &= -\frac{\cos \rho}{\rho} \\ n_1(\rho) &= -\frac{\cos \rho}{\rho^2} - \frac{\sin \rho}{\rho} \\ n_2(\rho) &= -\left(\frac{3}{\rho^3}-\frac{1}{\rho}\right)\cos \rho - \frac{3}{\rho^2}\sin \rho \end{align} 球ベッセル関数及び球ノイマン関数の無限遠方での漸近形は以下のようになる。
\begin{align} j_l(\rho) &\xrightarrow[\rho \to \infty]{} \frac{1}{\rho}\sin(\rho - l\pi /2) \\ n_l(\rho) &\xrightarrow[\rho \to \infty]{} \frac{1}{\rho}\sin(\rho - l\pi /2) \end{align} 一方、\(\rho\)が小さいときには以下で近似できる。
\begin{align} j_l(\rho) &\xrightarrow[\rho \to 0]{} \frac{\rho^l}{(2l+1)!!} \\ n_l(\rho) &\xrightarrow[\rho \to 0]{} \frac{(2l-1)!!} {\rho^{(l+1)}}\\ (2l+1)!! &\equiv 1\cdot3\cdot5\cdots(2l+1) \end{align} - 途中計算は以下の通り。
\begin{align} e^{ikz} &\rightarrow \frac{1}{kr}\sum_{l=0}^{\infty} (2l+1)i^{l} \sin(kr-l\pi /2)P_l(\cos \theta)\\ &= \frac{1}{kr}\sum_{l=0}^{\infty} (2l+1)i^{l} \frac{1}{2i}\left(e^{i(kr-l\pi /2)}-e^{-i(kr-l\pi /2)} \right) P_l(\cos \theta) \\ &= \frac{1}{2ikr}\sum_{l=0}^{\infty} (2l+1)i^{l} \left((-i)^l e^{ikr}-i^l e^{-ikr} \right) P_l(\cos \theta) \\ &= \frac{1}{2ikr} \sum_{l=0}^{\infty} (2l+1) \left(e^{ikr}-(-1)^l e^{-ikr} \right) P_l(\cos \theta)\\ \end{align} ちなみに正弦波をわざわざ\(e^{ikr}\)と\(e^{-ikr}\)で表しているのは、この方が扱いやすいからである。実際、このように表現することで正弦波が実際には内向き球面波と外向き球面波の合成から成り立っていることが分かる。 - 途中計算は以下の通り。
式(3.34)と(3.43)を式(3.42)に代入して漸近形を求めると
\begin{align} \Phi(r,\theta) &= \sum_{l=0}^{\infty} (2l+1) i^l e^{i\delta_l}\left(\cos\delta_l j_l(kr) - \sin\delta_l n_l(kr)\right) P_l(\cos \theta) \\ &\rightarrow \frac{1}{kr} \sum_{l=0}^{\infty} (2l+1) i^l e^{i\delta_l} \left(\cos\delta_l \sin(kr-l\pi /2) + \sin\delta_l \cos(kr-l\pi /2) \right) P_l(\cos \theta) \\ &= \frac{1}{kr} \sum_{l=0}^{\infty} (2l+1) i^l e^{i\delta_l}\sin(kr-l\pi /2+\delta_l) P_l(\cos \theta) \end{align} となり、式(3.41)と一致することが分かる。 - 以下のルジャンドル多項式の直交性を用いた。
\begin{align}
\int_{-1}^{1} P_l(z) P_{l'}(z) dz = \frac{2}{2l+1} \delta_{ll'}
\end{align}
ここで、\(\delta_{ll'}\)は、\(l=l'\)の場合だけ1になるクロネッカーのデルタである(\(l\neq l'\)のときはゼロ)。文中のように\(z=\cos\theta\)で表すと上記の積分は以下のようになる。
\begin{align}
\int_{-1}^{1} P_l(z) P_{l'}(z) dz &= -\int_{0}^{\pi} P_l(\cos\theta) P_{l'}(\cos\theta) \frac{dz}{d\theta} d\theta \\
&= \int_{0}^{\pi} P_l(\cos\theta) P_{l'}(\cos\theta) \sin\theta d\theta
\end{align}
\begin{align}
\therefore \int_{0}^{\pi} P_l(\cos\theta) P_{l'}(\cos\theta) \sin\theta d\theta = \frac{2}{2l+1} \delta_{ll'}
\end{align}
- 微分係数は運動量に相当するため連続的に接続しなければならない。
- 以下のように書けることから対数微分とも言う。 \begin{align} \frac{d \log f(r)}{dr} = \frac{1}{f(r)}\frac{d f(r)}{dr} \end{align}
- 絶対値の2乗なので\(|S_l-1|^2\)でも\(|1-S_l|^2\)でも結果は同じだが、慣例に合わせて\(|1-S_l|^2\)とした。
参考文献